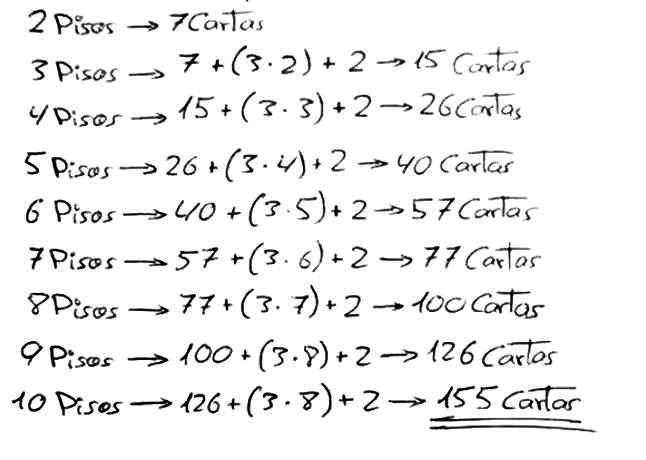Aunque el 14 de marzo es una buena fecha para proponer un poco de reflexión, no hace falta esperar al Día de Pi para llevar el tema al aula, poniendo en marcha actividades manipulativas que permitirán interiorizar mejor los aprendizajes.
Justo antes de que las restricciones por la pandemia de COVID-19 limitaran la actividad presencial en los centros, celebramos el Día de Pi mediante una actividad en la asignatura Didáctica de la Aritmética I, con alumnado de 2º curso del Grado de Magisterio en Primaria, en la Facultad de Ciencias Sociales y Humanas (UNIZAR) en Teruel.
Para ello, ambientamos la entrada del centro con materiales cedidos por los IES Salvador Victoria e IES Valle del Jiloca y realizamos un taller de cálculo de PI.

Sky-Line de Pi realizado por alumnado de 1º ESO del IES Valle del Jiloca
El objetivo era mostrar actividades alternativas que llevaran al alumnado (y al futuro alumnado de nuestro alumnado) a abordar contenidos matemáticos mediante actividades manipulativas, evitando la definición memorística de conceptos que se pueden introducir de manera más racional y dotando a los futuros maestros de herramientas para ello.
En concreto, puesto que estábamos cerca del día 14 de marzo, la actividad giró en torno al número irracional Pi y su presencia en diversos fenómenos, no solo asociados a la circunferencia. Le dedicamos una sesión de 2 horas de duración.
Comenzamos comentando su carácter irracional y trascendente, para pasar a explicar varios métodos para aproximar su valor, que a su vez muestran la variedad de fenómenos en que aparece esta constante. En concreto
- Como resultado del cociente entre la longitud y el diámetro de una circunferencia
- Como resultado de la división 22:7
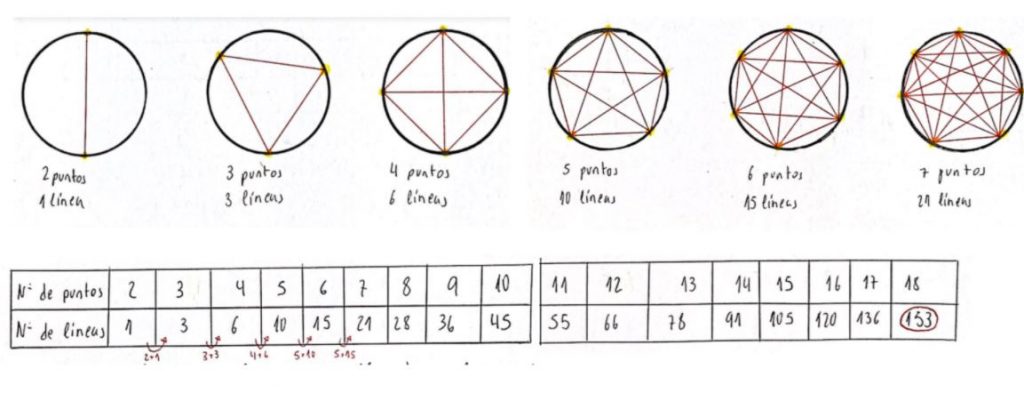
- Midiendo el diámetro de polígonos con un número cada vez mayor de lados
- Con la relación entre el área de un círculo y la del cuadrado en que está inscrito, con ayuda de números aleatorios
- Utilizando series, en concreto la resolución de Euler al Problema de Basilea
- Mediante la probabilidad, con el método de La Aguja de Buffon
Para ilustrar algunos de ellos, proyectamos vídeos. En el caso del primer método, vimos el vídeo PI con Pies, elaborado por el niño Lucas Fos para el concurso «Sin Pi no soy nada», dentro de la celebración del Pi Day Se trata de un estupendo ejemplo para llevar al aula.
Y para ilustrar otros, proyectamos el vídeo 3 Maneras de Saber que Pi=3.14159… , de QuantumFracture.
En una segunda parte de la sesión, organizados por grupos, se pusieron en marcha dos métodos de cálculo, poniendo en común al final los resultados de los distintos grupos, constatando la inexactitud de las medidas, pero también el clro acercamiento al valor real de Pi.
El primer método experimentado fue el primero, el cálculo como resultado del cociente entre la longitud y el diámetro de una circunferencia. Como material, se contó con diversos objetos de forma circular de varios tamaños, tiras de lana y reglas en centímetros y milímetros. Y por supuesto, una calculadora. Cada grupo hacía su cálculo con, al menos, dos objetos diferentes, y los resultados se iban escribiendo en una tabla común en la pizarra.




El segundo método experimentado fue el de La Aguja de Buffon, basado en que la probabilidad de que una aguja (cerilla en nuestro caso) toque una red unas líneas paralelas de anchura constante e igual a la longitud de la cerilla, es 2/Pi, por lo que 
Los grupos crearon sus plantillas con las rectas a distancia «una cerilla» unas de otras, lanzaron las cerillas e hicieron sus cálculos.



Cerramos la sesión con la proyección del corto Pipas, ganador del Premio al Mejor Guión y Premio TAI al Mejor director en la XI edición del festival Jameson Notodofilmfest
Esperamos que la realización de estas actividades en el aula, sencillas y con material manipulativo y accesible, muestren a estos futuros docentes las posibilidades que tiene el hecho de llevar la clase de Matemáticas más allá del lápiz y el papel.












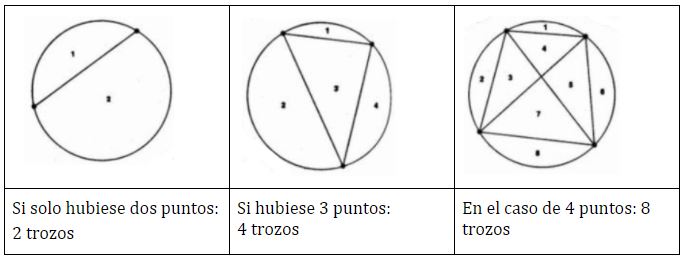
 La ronda de presos
La ronda de presos




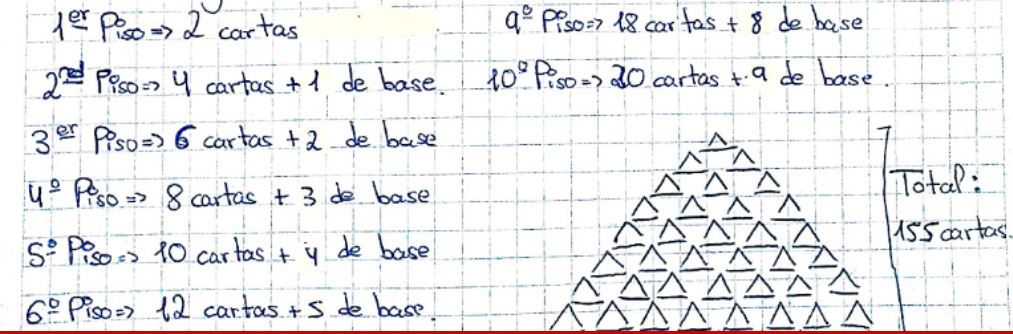
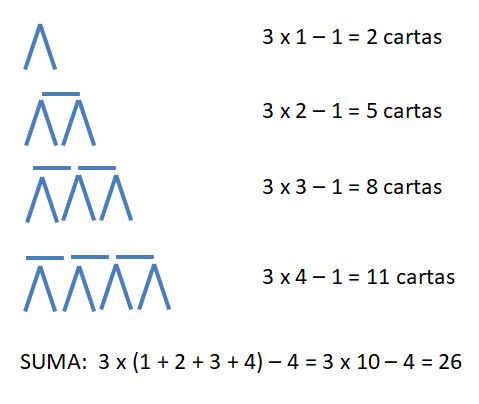
 Un clásico ejercicio de habilidad como el de construir castillos de naipes plantea un problema para llevar al aula: ¿Cuántas cartas son necesarias para construir un castillo de n pisos?
Un clásico ejercicio de habilidad como el de construir castillos de naipes plantea un problema para llevar al aula: ¿Cuántas cartas son necesarias para construir un castillo de n pisos?