 Un clásico ejercicio de habilidad como el de construir castillos de naipes plantea un problema para llevar al aula: ¿Cuántas cartas son necesarias para construir un castillo de n pisos?
Un clásico ejercicio de habilidad como el de construir castillos de naipes plantea un problema para llevar al aula: ¿Cuántas cartas son necesarias para construir un castillo de n pisos?
Entre las respuestas recogidas sorprende cómo se ataca la manera de contar las cartas. Aunque en algunos casos son similares, el desarrollo para llegar al resultado final varía. Veamos algunas de ellas.
Empezando por la parte superior, que sería el piso nº 1, se va formando la estructura hacia abajo. Este alumno empieza con las dos cartas, si solo hubiese un piso. Al construir otro piso se necesitan dos parejas de cartas y otra más para que el primero apoye; al edificar el tercero, se necesitan dos cartas para soportar el segundo además de las tres parejas que forman las construcciones de dicho piso, y así sucesivamente. Esta imagen lo ilustra:
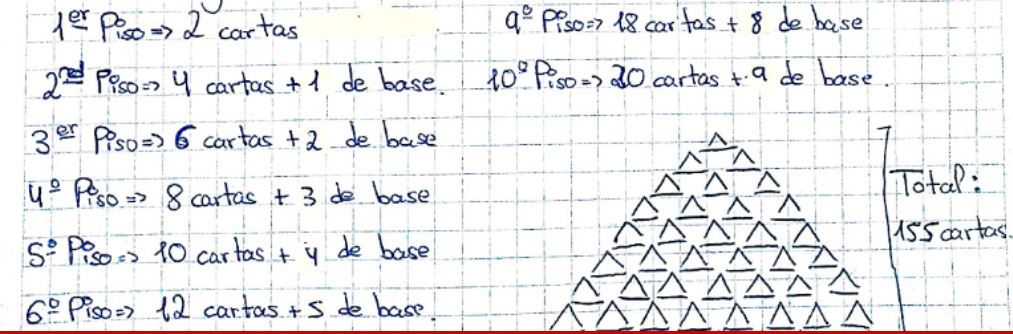
Aparecen dos progresiones aritméticas: 2, 4, 6, … y 0, 1, 2, … Basta sumar los n primeros términos de cada una de ellas para obtener el número total de cartas necesario para edificar del castillo de n pisos.
Por ejemplo, tal como se ve en la imagen, en el caso de 10 pisos, da como resultado 10·31/2=155.
Otra alumna plantea el recuento de las cartas desde una perspectiva de sustracción. Partiendo de grupos de 3 cartas (las dos laterales y la base) en cada piso harían falta 3 por el número del piso, pero habría que quitar las cartas que están en las bases, que son una menos del piso en el que estamos contando. Según esto, el proceso sería:
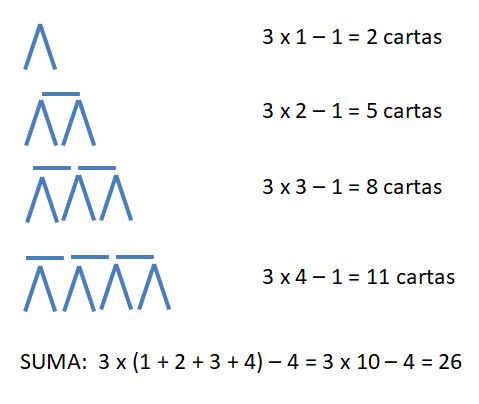
De manera que generalizando, para n pisos tendríamos:
Pero nos encontramos con otra manera de contar las cartas que nos lleva de nuevo a la solución del problema. El alumno que presenta esta solución aporta esta imagen para su explicación:

Como se ve, no cuenta cuantas hay en cada piso y luego suma, sino que va añadiendo, no un piso, sino apoyándose en lo anterior, completa por el lateral. Siguiendo este proceso, de manera numérica:
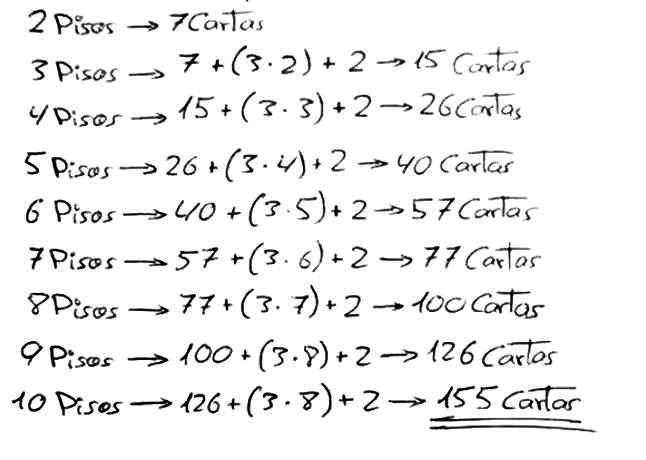
En esta secuencia se ve el procedimiento que le lleva a la solución, de manera recurrente. Llamando An al número de cartas que forman un castillo de n pisos, se tiene que:
¿Se te ocurre alguna otra manera de contar?
