Esther Ferrer es una artista donostiarra que incorpora matemáticas en su obra. Como ella dice, ayuda a visualizar las matemáticas desde el arte. Realizó una serie de obras a partir de lo que se conoce como el teorema de Napoleón:
Si sobre los tres lados de un triángulo cualquiera ABC se construyen tres triángulos equiláteros, los centros de estos tres triángulos equiláteros forman un nuevo triángulo también equilátero.

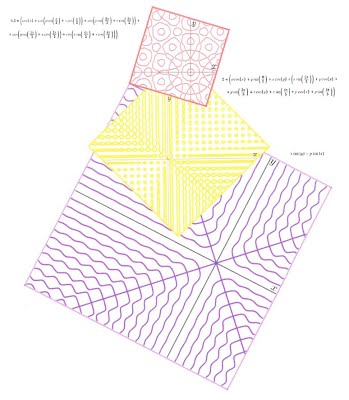
Esta idea es un buen punto de partida para llevarlo a otros resultados matemáticos. Así que se propuso a los alumnos de 1º de bachillerato, emular la idea con el teorema Finsler-Hadwiger:
Si dos cuadrados tienen un vértice común (A), los centros de ambos cuadrados (J y K) y los puntos medios (H e I) de los segmentos (BE y DF) que unen los vértices respectivos adyacentes al común forman otro cuadrado.
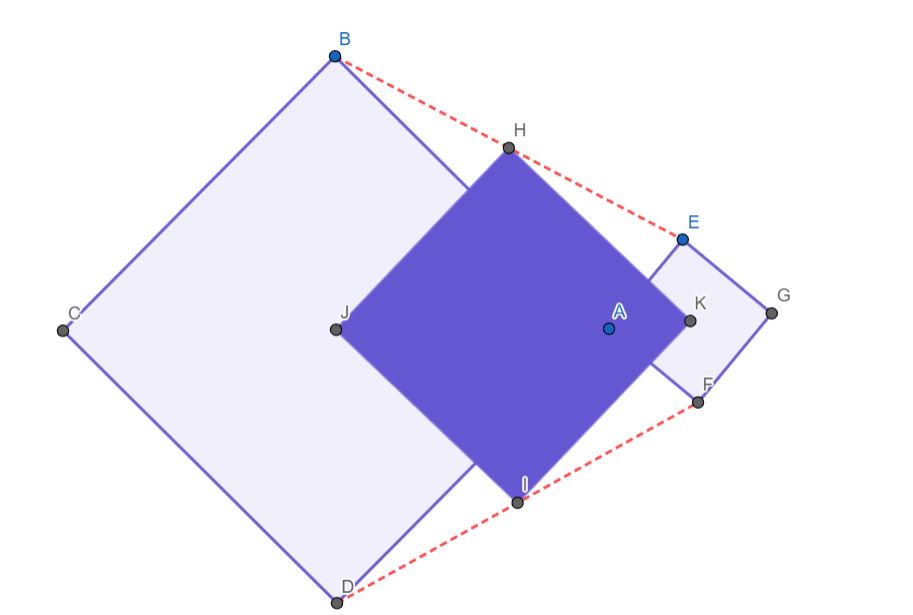
El primer paso fue realizar la construcción con GeoGebra a partir del enunciado y comprobar que se cumple el teorema. A partir de ahí, buscando una disposición de los cuadrados a su gusto, los decoraron. Algunos de los resultados presentados fueron estos: