La ronda de presos, es un cuadro que Vincent van Gogh pintó en 1890, durante su estancia voluntaria en el sanatorio Saint-Rémy-de-Provence. Se trata de una interpretación del grabado London: A pilgrimage de Gustave Doré.
En el lienzo se ven 33 presos que caminan en círculo en el patio de la prisión bajo la mirada de tres personas. El cuadro sirvió de excusa en la clase, para plantear un problema de posición: el problema de Flavio Josefo. La adaptación a este cuadro, tal como se presentó al alumnado fue la siguiente:
“Imagina que tú estás entre los presos. Ha llegado una notificación del gobernador de la prisión para que uno se salve, pero la manera de seleccionar al afortunado va a seguir un procedimiento curioso:
Empezando por el preso rubio (1) que mira al frente, este toca al preso que tiene delante, el 2, y eso ya condena al 2 a quedarse en la cárcel. A continuación el 3, que no ha sido tocado todavía, toca al que tiene delante (el 4) y este se queda… y así sucesivamente. Cuando llegue al 33, tocará al 1, que se quedará, y vuelta a empezar. El primero que todavía tiene posibilidades de ser liberado (en este caso el 3) toca al siguiente en sus mismas condiciones, es decir, el 5, y el 7 tocará al 9 y todo el proceso se repite hasta que haya uno que no haya sido tocado por nadie. Ese es el que saldrá libre.
¿En qué posición deberías colocarte para saber con seguridad que vas a ser el agraciado que saldrá libre?
¿Y si en lugar de 33 presos fueran 34 o 41 o 57 o 64 o n?”
Comenzando con casos más sencillos, van elaborando hipótesis sobre el lugar en el que hay que colocarse para eludir la cárcel:
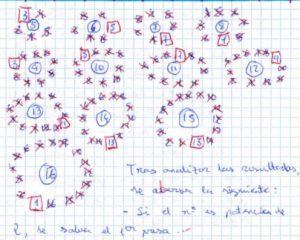
Continúan con sus apreciaciones de la siguiente manera:
Una vez encontrados los patrones, la dificultad se centra en explicarlos y resumirlos en una expresión que permita saber la posición adecuada para salir airoso de este círculo.
donde n representa el número de presos y x la potencia de 2 más cercana, por defecto, de n.
O bien:
El cuadro Ronda de presos, sirvió para plantear otros tipos de problemas que ya se han comentado en este blog: Uniendo puntos y A trozos.
