En estos días les propuse a los alumnos un problema muy conocido: ¿Cuántos segmentos se generan al unir entre sí 18 puntos colocados sobre una circunferencia?
Entre las respuestas enviadas, los procedimientos aportados para la resolución y generalización del problema, recorren tres vías: la recurrencia, la suma de los n primeros números naturales y la obtención de una expresión algebraica, el término general.
Una de las maneras de atacar un problema como este consiste en empezar por casos sencillos. Así, una alumna fue poco a poco aumentando el número de puntos y encontrando una recurrencia: «me di cuenta que la suma de puntos y líneas da el número de líneas del siguiente número de puntos».
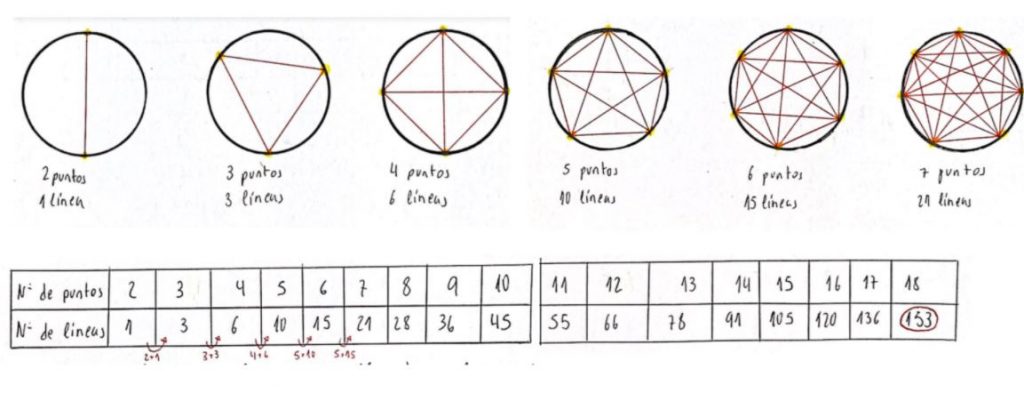
De esta manera resuelve el problema planteado con 18 puntos. Encontrar el número de segmentos para un número elevado de puntos supondría un buen rato de cálculos pero podría buscar una generalización del tipo , aunque no lo hace.
En otro de los documentos presentados, otra alumna cambió el enfoque:

De la misma manera que antes, un número más elevado de puntos hubiera proporcionado un buen rato de cálculo de las sumas, que se podría evitar planteando la suma de los n primeros números naturales como solución que generaliza el problema: .
Y de nuevo, un cambio de enfoque nos lleva a una generalización del problema con este razonamiento:

No fueron casos únicos, los alumnos se repartieron estos caminos para dar respuesta al problema.
