Mar 06 2017

Puzzles de áreas

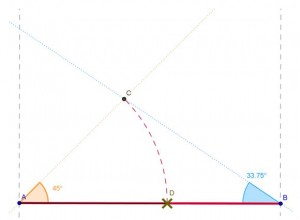
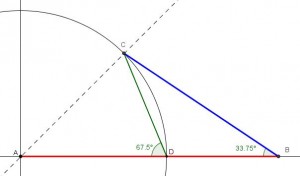
Cada semana propongo a mis alumnos un desafío. Son muy variados y procuro ir salteando tipos de contenidos distintos. Internet es de gran ayuda para la búsqueda de nuevas propuestas y formatos. Es el caso de los Area Maze  o Puzzles de áreas. Los comenzó a crear el japonés Nooki Inaba,  y su popularidad ha ido creciendo, tras la publicación en The Guardian de un artículo dedicado a ellos, en el que se explican en un breve video.

 

En la actualidad se ha publicado en España un libro que recoge algunos de ellos para niños (Rompecabezas lógicos de áreas MENSEKI MEIRO para niños). Puedes encontrar una colección de sitios en los que aparecen estos puzzles en este enlace, así como una versión digital en este otro. También hay una app para móviles que propone este tipo de retos.

La peculiaridad de esta propuesta es que hay que encontrar el valor de lo que se pide (puede ser un segmento o un área) utilizando nada más que números enteros. Esta semana el desafío con el que reté a mis alumnos fue este:

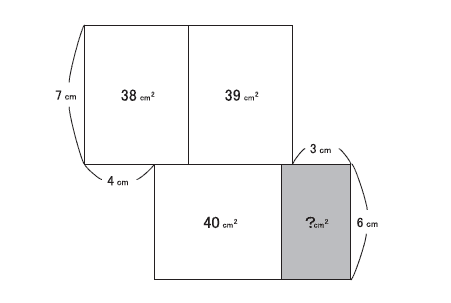
No resulta de una excesiva complejidad, pero me ha sorprendido que me han entregado cinco formas distintas de resolverlo. Algunas son similares pero incluyen matices que las hacen diferentes.

Iván ha prolongado los lados que quedan en el interior y ha ido descomponiendo en rectángulos más pequeños los dados, buscando sus áreas. El objetivo era encontrar el área del rectángulo estrecho que forma parte del buscado (que él ha señalado como área 4). Sara ha perseguido el mismo fin, aunque ha llegado por un camino un poco diferente.

 

 

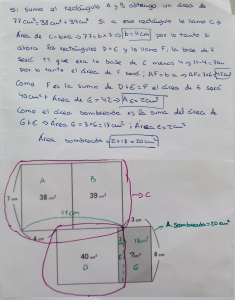
Óscar y Javier (con algún fallo en la escritura), aunque han comenzado como Sara, han continuado por otro camino:

Por último, Alejandro ha utilizado la figura completada, es decir, ha añadido los rectángulos de los que solo hay dos lados en los extremos y eso le ha servido para llegar a la solución.

Mar 02 2017

Serie microrrelatos-2: Fin numérico

111, 222, 333, 444, 555…

Estos eran los números que resultaron asignados a aquellos pobres desgraciados, los cuales eran inocentes y la justicia los declaró criminales.

El único crimen que cometieron fue fallecer.

La parca se los llevó, sin preguntar… 1, 2, 3…

Lentamente caían en brazos de la perfecta sombra del infinito, la cual ni rencor ni alma poseía, y su único objetivo fue restar…

Restar felicidad.

Joana Cortés Picornell  2ºESO

IES Valle del Jiloca

Feb 26 2017

Aplicación práctica de la formula de Herón

Durante este curso 2016-17, desde el departamento de biología y Geología del IES Valle del Jiloca, se está desarrollando el proyecto “Parque agrícola de los secanos del Jiloca“. Su objetivo es estudiar, mediante la práctica, el desarrollo de diferentes tipos de plantas herbáceas que tradicionalmente se han cultivado en la zona.
Para ello, han delimitado parcelas en un terreno adjunto al centro y han sembrado varios tipos de semillas.
Entre otras cosas, han tenido que calcular la densidad de semillas esparcidas por las parcelas, para lo cual, han tenido que calcular el área de las mismas. Dado que no eran polígonos regulares, desde el departamento de Matemáticas se les sugirió la posibilidad de usar la Fórmula de Herón.
El proyecto va quedando reflejado en su blog Parque agrícola de los secanos del Jiloca, y aquí reproducimos el trabajo de uno de los grupos:

 

El pasado día 27 de enero fuimos a las parcelas del Parque Agrícola de los Secanos del Jiloca para calcular la superficie de las diferentes especies sembradas anteriormente. Una de ellas fue la veza villosa.
 
 
Las parcelas eran cuadriláteros irregulares. Para calcular su superficie se dividieron en dos triángulos trazando entre dos vértices no consecutivos una diagonal. Tomamos cinco medidas: la de los cuatro lados y la diagonal que pasa de un vértice a otro. Posteriormente utilizando la fórmula de Herón calculamos el área de cada uno de los dos triángulos, conociendo la longitud de sus tres lados a, b y c.
 

 

DENSIDAD: MASA / SUPERFICIE
Medidas de la parcela de la veza

Perímetro triángulo 1: 9,83 m
Perímetro triángulo 2: 9,905 m
Superficie triángulo 1: 15,250 m2
Superficie triángulo 2: 15,821m2
Superficie total: 31,071 m2 = 0,0031 hectáreas
Finalmente, calculamos su densidad:
Veza plantada: 0,22 kg
Densidad: 0,0071 kg/m2 = 70,81 kg/hectárea      

 

 

Si comparamos la cantidad de veza que se ha plantado en nuestro centro, con la cantidad de semillas que normalmente se usa para la siembra que es de 70 kg/hectárea si es para obtener siembra y de 125 kg/hectárea si es para producir forraje, observamos que hemos empleado una cantidad muy escasa de veza en nuestro instituto.

 
Xue Ru Xu, Claudia Roza, Carmen Sebastián, Alicia Villalta y Adnana Dragut
4º ESO, IES Valle del Jiloca – Calamocha
 

Feb 22 2017

Pasión por las matemáticas

Viajo poco a Zaragoza (vivo en un pueblo de Teruel) y cuando lo hago siempre es por cuestiones prosaicas, pero este fin de semana pude sacar un hueco y aprovechar para visitar la exposición  sobre Zoel García de Galdeano, que se ha  podido contemplar en el Paraninfo de la Universidad de Zaragoza hasta el 28 de febrero. Esta exposición ha sido organizada con motivo del Congreso Bienal de la Real Sociedad Matemática Española que se celebró en Zaragoza del 30 de enero al 3 de febrero.

 

En realidad han sido dos exposiciones. En la instalada en la preciosa biblioteca del Edificio Paraninfo, bajo el título de Zoel García de Galdeano: un legado de progreso matemático, se ha podido contemplar una colección de obras impresas sobre matemáticas entre los siglos XVI y XIX, que muestran un recorrido por la historia de las matemáticas. Gran parte de estas obras forman parte del legado que García de Galdeano hizo a la Facultad de Ciencias. El catálogo de las obras expuestas se puede ver en este enlace.

 

En una sala cercana la exposición Zoel García de Galdeano: pasión por las matemáticas muestra documentos académicos, publicaciones, modelos de superficies, así como detalles de la biografía y trayectoria profesional e incluso el testamento de García de Galdeano.

Zoel García de Galdeano participó de forma habitual en congresos internacionales, fue uno de los pocos matemáticos españoles que asistió al famoso II Congreso Internacional de Matemáticos en París (1900). Realizó una gran labor de actualización matemática en España a través de sus trabajos de divulgación. Fue director de El Progreso Matemático, primera revista de matemáticas publicada en España, que él mismo fundó en 1891. Posteriormente, en 1914 impulsó la creación de la Real Academia de Ciencas Exactas, Fìsicas, Químicas y Naturales.

 

Julio Rey Pastor, su alumno, dijo de él:

 

Esta entrada participa en la Edición 8.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.

 

Feb 19 2017

Semana Matemática en el IES Salvador Victoria

La semana del 6 al 10 de febrero de 2017 celebramos en el IES Salvador VIctoria de Monreal del Campo la semana matemática de este curso. Junto con los talleres y charlas hemos podido contemplar dos exposiciones: la que ofrece el programa Conexión Matemática, que en esta ocasión ha sido “Naturales, como tú” y otra elaborada por todos los alumnos del centro en torno al reloj, ya que este curso el proyecto central de nuestro centro es Kronosferia (dedicado al tiempo cronológico). Y como actividad estrella del recreo, hemos construido un omnipoliedro.

Toda la información sobre las actividades de la semana, en este enlace.

Feb 15 2017

Los tres pintores

Nuevo cuento interactivo de Matematicinfantil. Tres pintores que solo saben pintar cada uno con una única forma geométrica se unen para pintar un gran cuadro para el cole. Está dirigido a niños de 3 a 5 años, y se puede acceder a él pinchando sobre la imagen.

En el blog de Matematicinfantil se recogen indicaciones para su uso así como orientaciones metodológicas.

Feb 12 2017

Semana Matemática 2016-2017 en el IES Valle del Jiloca

Entre el 30 de enero y el 3 de febrero pasados, se celebó en el IES Valle del Jiloca (Calamocha – Teruel) la Semana Matemática, en colabración con el programa Conexión Matemática.

Hubo talleres para los diferentes cursos, actividades durante el recreo, exposiciones… En suma: posibilidades de ver las matemáticas desde una óptica diferente.

Si quieres ver el resumen de la actividad, ilustrada con fotografías, consulta la página web:

 

Feb 08 2017

Las posibilidades del triángulo de Pascal

El alumnado de 1º de Bachillerato de Ciencias y Tecnológico del IES Valle del Jiloca trabajó el artículo Los tesoros matemáticos que esconde el triángulo de Pascal, de Miguel Ángel Morales, publicado el pasado 2 de noviembre en El Aleph.

Tras una lectura detallada y las aclaraciones de todos los aspectos que lo requirieron, trabajndo en pequeños grupos elaboraron los paneles de la exposición “El triángulo de Tartaglia: ¿Qué esconde?“

 

Los paneles, ya en su ubicación definitiva:

Feb 05 2017

II Jornada de Educación Matemática en Aragón

Este fin de semana pasado, durante la tarde del viernes 3 y la mañana del 4 de febrero de 2017, se ha desarrollado en la Facultad de Educación de Zaragoza la II Jornada de Educación Matemática en Aragón.

Cerca de 200 profesores inscritos han participado en las distintas actividades programadas: 3 sesiones plenarias, 3 sesiones de comunicaciones breves de experiencias con 6 de forma simultánea en cada franja horaria y un taller entre 6 ofertados. Además se ha dedicado un recuerdo a Ángel Ramírez, ponente que clausuró la I JEMA.

Se han podido contemplar cuatro exposiciones: Cuadrando ideas y Naturales, como tú, del programa Conexión Matemática, los 17 grupos de simetría en el mudéjar aragonés de Carlos Usón y Ángel Ramírez, y Enigmáticos caminos geométricos de Ligia Unanue.

Además se contó con una serie de carteles de trabajos de alumnos del IES Batalla de Clavijo (Logroño), un póster del trabajo realizado en Infantil en el CEIP San Juan de la Peña (Jaca), y con dos trabajos de hiloramas de alumnos del IES Salvador Victoria (Monreal del Campo). El CRIE de Zaragoza montó un mural sobre el conocido mosaico de lagartos de Escher, comenzado con los alumnos del centro y en el que quien quiso pudo pegar su lagarto para continuar el mural.

Como complemento también se dispusieron dos mesas, una sobre JumpMath y otra con el cómic Dudas, axiomas y navajas suizas.

Toda la información de la Jornada se puede ver en la página web. En el blog de la Sociedad Aragonesa de Profesores de Matemáticas, organizadora del evento se puede leer una crónica del mismo.

Fotografías de José Mª Sorando

Ene 29 2017

Proporción cordobesa

La relación que existe entre el radio y el lado  de un octógono regular se conoce con el nombre de proporción cordobesa o número cordobés. Su valor decimal es c= 1,30656…

cordobesa

 

Aunque se puede expresar de forma más precisa con la expresión radical c=\frac{1}{\sqrt{2-\sqrt{2}}}

cordobesa1

O la expresión trigonométrica c= \sqrt{2}cos22^{\circ} 30.

 

cordobesa2

 

O de forma más sencilla por la propia definición del seno aplicado en el triángulo del dibujo:

 

 

\displaystyle\ \frac{l}{r}=2sen\frac{\pi}{8}

 

\displaystyle\ c=\frac{r}{l}=\frac{1}{2}cosec\frac{\pi}{8}

 

 

 

Si queremos construir un rectángulo con esas proporciones basta hacer esto:

 

cordobesa3

 

¿Y cómo dividimos un segmento dado en la proporción cordobesa? Aquí se muestra un sencillo y rápido método.

Se dibuja desde un extremo A un ángulo de 45º y desde el otro, B,  un ángulo de 33,75º. La distancia desde A hasta C (punto en el que se cortan los segmentos anteriores) se lleva sobre AB y obtendremos la partición del segmento en proporción cordobesa.

cordobesa4

 

Vamos a justificar la construcción. Partimos de un segmento AB, y buscamos un punto D en el segmento tal  que la relación entre AD y DB sea la proporción cordobesa. Por la propia definición del número cordobés como relación entre el radio y el lado de un octógono, la división de AD entre CD es precisamente ese número. Ello quiere decir que el triángulo BCD es isósceles pues CD y DB son iguales. Por otro lado, el ángulo ADC mide 67º 30′ ya que ACD es isósceles y  el ángulo ADC mide 45º.  Así pues uniendo ambos resultados, obtenemos que el ángulo DBC ha de medir la mitad de ADC, o sea 33º 45′. Con lo cual se comprueba que la construcción es correcta.

cordobesa5

Quizá el ángulo 33,75º resulte un poco caprichoso, pero su construcción solo necesita de dibujar tres bisectrices partiendo de un ángulo recto. La primera nos determina el ángulo de 45º, la segunda el de 22,5º y por último se biseca el ángulo que forman las dos bisectrices anteriores y conseguimos el ángulo buscado.

cordobesa6

 

Este post participa en la Edición 7.X del Carnaval de Matemáticas cuyo anfitrión es el Blog del IMUS.