Oct 14 2016

Matemáticas para marcar tortugas.

 

El pasado mes de octubre, realizamos un intercambio de alumnado con un centro de la localidad francesa de Sousons (Landes –

Imagen de www.berryprovince.com

 

Aquitania).Entre otras actividades, realizamos una visita guiada a la Reserve naturelle de L’Etang Noire, situado en Seoignosse, al sur de Soustons.
El objetivo de la visita era conocer la diversidad biológica del enclave, para lo cual contamos con la compañía del guía (Matieu) que nos mostró el lugar de forma eficaz, amena y agradable.

Hacia el fnal de la visita, centró sus observaciones en una especie presente en el lugar y sobre la que están realizando un estudio: la cistude, una especie de galápago (tortuga) acuática.

Matieu nos explicó el método de investigación que utilizan para conocer la población de tortugas que tienen en el pequeño Etang Noire. Capturan a los individuos medante trampas de red, y los miden: longitud, anchura y peso. Estiman su edad (por los «casi-cuadriláteros» concéntricos del caparazón) y su sexo (por el color de los ojos: amarillos las hembras y rojos los machos). Todos estos datos son anotados en una ficha y después se debe devolver al agua. Pero, ¿Cómo reconocerla si se vuelve a capturar?

cistude1

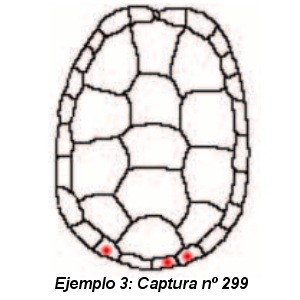
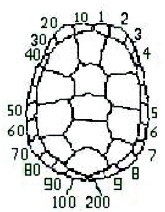patronEl método, en realidad, reproduce un sistema de numeracón decimal. Se basa en el hecho de que todos los ejemplares tienen la misma estructura poligonal en el caparazón. Se marcan con pintura hasta tres de estos polígonos con el siguiente criterio:

  • Desde la marca cenral donde está la cabeza hacia la derecha se cuentan las unidades. Se excluyen dos áreas asociadas a la osificación del caparazón.
  • Desde esa misma marca hacia la izquierda, se cuentan las decenas (se excluye la misma parte).
  • Las dos marcas inferiores, junto a la cola, marcan el 100 y el doscientos.

De este modo, se pueden marcar hasta 299 tortugas, cantidad, en principio, superior a la población del estanque. Los datos son recogidos en fichas individuales como esta:

 

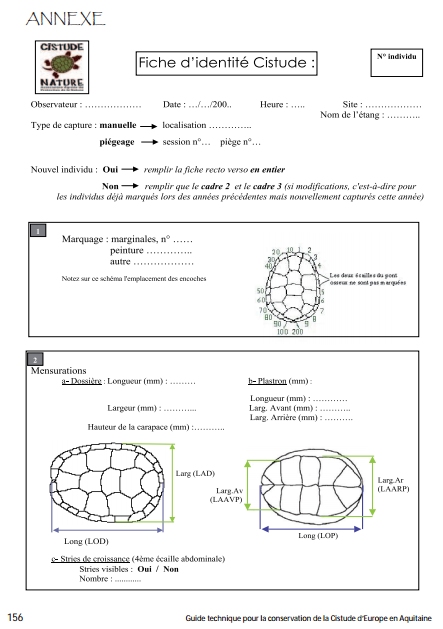
ficha

Obtenido del documento «Guide technique pour la conservation de la cistude d’Europe en Aquitanie» http://www.cenlr.org/sites/www.cenlr.org/files/documenst_communs/pdf/cistude/PRIOL_Cistude_guide_Aquitaine.pdf

Algunos ejemplos de marcaje podrían ser estos:

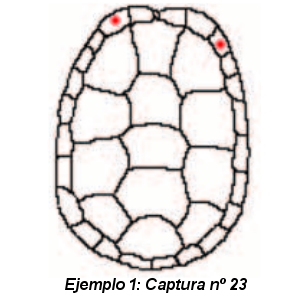
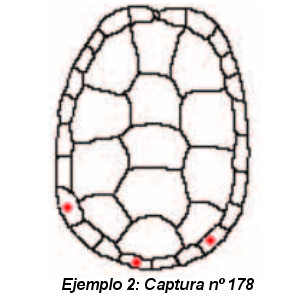
captura23 captura178 captura299

En el transcurso de la visita los alumnos pudieron simular la captura de una de estas tortugas y poner en práctica el método de medida y marcaje de la misma. Fue una experiencia muy interesante.

cistude3

cistude2

 

Oct 11 2016

WODB

FaceTweet it!

WHICH ONE DOESN’T BELONG?  es un recurso muy interesante para el aula.
Una imagen muestra cuatro elementos, bien sean formas, números, gráficas, imágenes, etc., y  el objetivo es encontrar cual de ellos no encaja con el resto. La respuesta puede ser cualquiera de los cuatro. Esto es lo que hace interesante esta propuesta pues hay que encontrar elementos comunes y distintos entre lo que se ve.

Por ejemplo, en esta cuadrícula, por una cuestión de sombreado, rápidamente encontramos una justificación para decir que el triángulo gris es el que no encaja, pero si nos fijamos en el número de lados de los polígonos, quien no debería estar ahí es el hexágono. Quizá sea un poco más complicado encontrar razones para los otros dos triángulos. En el caso del isósceles, una razón podría ser que todos los polígonos tienen al menos un ángulo igual o mayor de 90 grados. Y, un poco rebuscada, pero una razón para señalar al escaleno podría ser que el centro de la circunferencia circunscrita a estos polígonos se encuentra fuera de él, a diferencia de lo que ocurre en los otros tres.
Un ejercicio aparentemente sencillo que requiere de múltiples puntos de vista. Muy interesante.

 

Oct 08 2016

Volver a empezar

Hace un tiempo que llevamos preparando la vuelta de Matryc y por unos motivos u otros ha ido demorándose más allá de lo previsto.

Hemos reordenado un poco la estructura y el aspecto con la intención de darle un aire renovado. Las secciones del menú Mareriales (Interactivos, Multimedia, Manipulables e Imprimibles) responden a un criterio más metodológico que de contenidos. Y elevamos Lecturas a la categoría de sección, dado que mantenemos nuestra idea de la importancia de la lectura al aprender y enseñar Matemáticas.

Para acceder a los contenidos de la página según los bloques temáticos los niveles educativos o la tipología de los materiales comentados, mantenemos el menú Por bloques en la barra lateral.

Como hemos cambiado de alojamiento vamos poco a poco pasando todas las entradas anteriores que nos parece interesante que estén disponibles aquí. Es un trabajo largo, que ya hemos comenzado.

Con este vídeo de la cantante francesa Jain queremos comenzar esta nueva etapa, con ilusiones (las suyas, ópticas), buen ritmo (esperamos que lo marque la regularidad de nuestras entradas) y buen humor. Bienvenidos de nuevo a Matryc.

Jun 14 2016

Pobre cartero

 

cartero

Jun 14 2016

Códice Atlanticus

Folio 471v del Codice Atlanticus con Geogebra:

 

 

 

May 15 2016

Raíz cuadrada

Un amigo me pasó hace poco este video:

 

En él se explica un método para calcular la raíz cuadrada de un número por aproximación, el método  babilonio. Se trata de ir ajustando rectángulos de área el número propuesto,  para conseguir un cuadrado. Partiendo de un rectángulo de esa área, para la siguiente iteración se toma la semisuma de los lados como nuevo lado del siguiente rectángulo y se busca el valor del otro y así sucesivamente.

Me puse a visualizarlo realizando el proceso con Geogebra y se consigue una buena aproximación al resultado con muy pocos pasos. ¿Con qué número comenzamos la primera iteración? Por mantener el criterio de ir diviendo entre dos la suma de los lados, elegí la mitad del número propuesto como valor inicial. Probé con otros y da mejor resultado el valor medio.

 

 

El aplet se puede ver en este enlace.

En la columna A se van calculando los valores de uno de los lados del rectángulo. En A1:k/2. En B1 se calcula cuanto valdrá el otro lado del rectángulo para que el área sea k. En este primer paso es claro que 2.

A continuación se calcula A2 como la semisuma de A1 y B1, y en B2 calculamos el lado del rectángulo de área k cuyo otro lado es A2, y así sucesivamente.

En la columna C se dibujan los rectángulos de lados A1 y B1, A2 y B2, etc.

Si el número de partida en A1 está cercano al valor de la raíz, la convergencia es, obviamente, mucho más rápida.

Los vértices superiores de la derecha de cada uno de los rectángulos se corresponden con puntos de la función y=k/x. El punto que dará la solución, o sea el valor de la raíz cuadrada, será aquel cuyas dos coordenadas sean iguales (tendremos entonces el cuadrado) y ese punto pertenecerá a la recta y=x.

Es decir el valor de la raíz cuadrada de k se obtendrá en la intersección de las gráficas de y=k/x e y=x

 

 

Abr 20 2016

Círculos con en-Cantor

Partiendo de un círculo de radio R,  aplicamos la construcción del conjunto de Cantor al diámetro y en cada segmento que se suprime se dibuja un círculo. Obtenemos la siguientes figuras:

   

    

¿Qué fracción de la superficie del círculo original queda pintada de azul si se repite el proceso indefinidamente?

Partimos de un círculo de radio R, por tanto diámetro 2R. Se divide este en tres partes y sobre la tercera, de radio R/3, se construye un círculo y se repite el proceso con los segmentos que van quedando del diámetro original.  El área de los círculos que se van suprimiendo en cada uno de los pasos será:

Y en el paso n-ésimo:  

 

De manera que en total el área que se suprime es la suma de todas las áreas anteriores, que no es más que la suma infinita de una serie geométrica.

 

Volviendo a la parte gráfica, dibujamos un círculo de radio R, y construimos siguiendo el procedimiento de la espiral de Teodoro, el segmento de longitud raíz de siete, que lo dividimos en siete partes:

Dibujamos el círculo de centro A y radio hasta la primera de las siete partes:

Y sobre esta corona circular, utilizando uno de los procedimientos comentados en la entrada «Corona circular» de este blog, permite dibujar el círculo con la misma área que la corona que representa los seis séptimos del círculo original.

Esta entrada participa en la ‘edición 6.9: el conjunto de Cantor‘ del Carnaval de Matemáticas, cuyo blog anfitrión es ::ZTFNews;

Abr 15 2016

Ley de los grandes números

A la hora de abordar de una forma visual la Ley de los grandes números, existen aplicaciones que permiten repetir el lanzamiento, por ejemplo de un dado, una elevada cantidad de veces y ver como las frecuencias relativas se van igualando. Si se quiere hacer la experiencia en directo en clase, nos encontramos con el problema de recopilar todos los datos. Cada alumno puede repetir 20 veces el lanzamiento del dado, se anotan los resultados, y se va elaborando una tabla en la pizarra. Hasta que no están todos los lanzamientos realizados no se puede ir confeccionando esa tabla.

Las tecnologías actuales nos permiten realizar esto mismo en directo y ver en cada instante como va variando esa tabla y como evoluciona un gráfico de barras que recoja la información.

 

 

¿Cómo? Preparamos un formulario de Google con el que se podía introducir el resultado de cinco tiradas. Cada alumno (o por parejas) dispone de un ordenador y un dado con el que realizar el experimento, durante unos diez minutos. Este tiempo es suficiente para llegar a unas 2000 tiradas en total. Una vez introducidos los datos, se recogen en una hoja de cálculo asociada al formulario en la que previamente se ha preparado una tabla que cuenta el número de veces que ocurre un resultado en un rango de celdas lo suficientemente grande para que quepan todos los envíos producidos en la clase. Con esa tabla de frecuencias se inserta un gráfico de barras y ya está. Conforme van entrando los resultados de los formularios que se van enviando, se puede observar cómo varían tanto la tabla de frecuencias como el gráfico.

 

 

En nuestro caso, tras 2000 tiradas, se llegaron a igualar las frecuencias de todos los números excepto el dos. Aunque visualmente parece que destaca mucho el resultado del 2, un análisis de las frecuencias relativas obtenidas muestra que no es tanto. En esta ocasión hubiésemos necesitado muchas más tiradas para llegar a que se igualaran las frecuencias, pero tocó el timbre…

Abr 06 2016

Leonardo y Luca

Leonardo y Luca, una sólida relación, es una exposición que aborda los cinco sólidos platónicos, sus truncamientos y elevaciones, partiendo de los dibujos que Leonardo da Vinci realizó para ilustrar el libro La divina proporción de Luca Pacioli.

La exposición consta de ocho carteles. Se acompaña de un cuadernillo de actividades y unos materiales fotocopiables para poder recortar y construir determinados cuerpos geométricos que permiten realizar algunas de las propuestas. Para completar la exposición se ha creado una página web en la que se pueden descargar los materiales y además disponer de otras actividades, así como de informaciones para ampliar y profundizar.

 

Mar 15 2016

La mitad de un círculo

Hay muchas maneras de dividir un círculo en dos partes iguales. Algunos casos son evidentes en ciertos logotipos como por ejemplo:

        Con un poco de tiempo encontramos muchas formas de partir el círculo en dos:

 

Geogebra nos permite investigar algunas otras maneras de hacerlo. Una de ellas es la de cortar un sector, un quesito. En este aplet se puede ir moviendo el punto e ir buscando donde debería colocarse consultando las áreas que va calculando el programa: la del círculo y la del trozo que vamos creando.

Si activamos el rastro, se irá coloreando de azul aquellos puntos que dan la solución al problema y activando la casilla de solución, aparecerá el lugar geométrico de todos los puntos solución.

Si se activa la animación automática del aplet, un escáner barrerá todo el círculo e irá apareciendo la solución ante nuestros ojos.