Ene 29 2017

Proporción cordobesa

La relación que existe entre el radio y el lado  de un octógono regular se conoce con el nombre de proporción cordobesa o número cordobés. Su valor decimal es c= 1,30656…

cordobesa

 

Aunque se puede expresar de forma más precisa con la expresión radical c=\frac{1}{\sqrt{2-\sqrt{2}}}

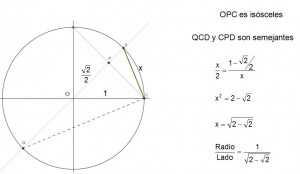
cordobesa1

O la expresión trigonométrica c= \sqrt{2}cos22^{\circ} 30.

 

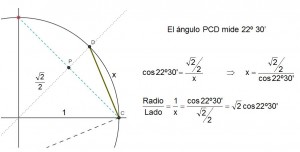
cordobesa2

 

O de forma más sencilla por la propia definición del seno aplicado en el triángulo del dibujo:

 

 

\displaystyle\ \frac{l}{r}=2sen\frac{\pi}{8}

 

\displaystyle\ c=\frac{r}{l}=\frac{1}{2}cosec\frac{\pi}{8}

 

 

 

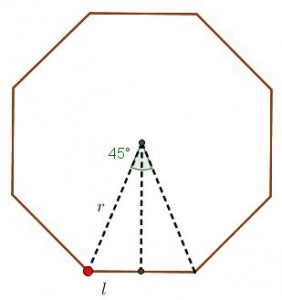
Si queremos construir un rectángulo con esas proporciones basta hacer esto:

 

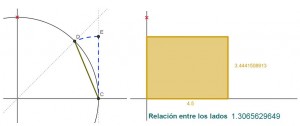
cordobesa3

 

¿Y cómo dividimos un segmento dado en la proporción cordobesa? Aquí se muestra un sencillo y rápido método.

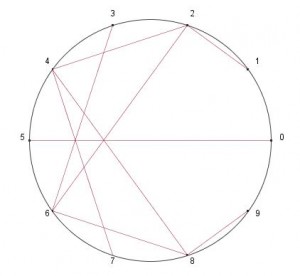
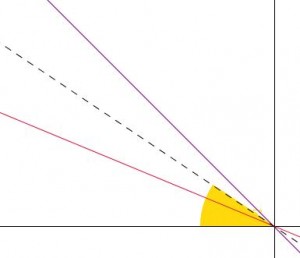
Se dibuja desde un extremo A un ángulo de 45º y desde el otro, B,  un ángulo de 33,75º. La distancia desde A hasta C (punto en el que se cortan los segmentos anteriores) se lleva sobre AB y obtendremos la partición del segmento en proporción cordobesa.

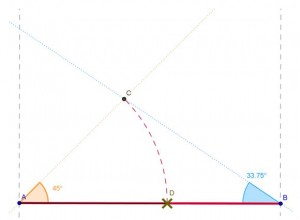
cordobesa4

 

Vamos a justificar la construcción. Partimos de un segmento AB, y buscamos un punto D en el segmento tal  que la relación entre AD y DB sea la proporción cordobesa. Por la propia definición del número cordobés como relación entre el radio y el lado de un octógono, la división de AD entre CD es precisamente ese número. Ello quiere decir que el triángulo BCD es isósceles pues CD y DB son iguales. Por otro lado, el ángulo ADC mide 67º 30′ ya que ACD es isósceles y  el ángulo ADC mide 45º.  Así pues uniendo ambos resultados, obtenemos que el ángulo DBC ha de medir la mitad de ADC, o sea 33º 45′. Con lo cual se comprueba que la construcción es correcta.

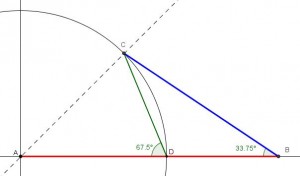
cordobesa5

Quizá el ángulo 33,75º resulte un poco caprichoso, pero su construcción solo necesita de dibujar tres bisectrices partiendo de un ángulo recto. La primera nos determina el ángulo de 45º, la segunda el de 22,5º y por último se biseca el ángulo que forman las dos bisectrices anteriores y conseguimos el ángulo buscado.

cordobesa6

 

Este post participa en la Edición 7.X del Carnaval de Matemáticas cuyo anfitrión es el Blog del IMUS.

 

Ene 26 2017

Sobre Galois

A partir del artículo «Galois, el matemático que se convirtió en genio antes de los 21 años», de F. Corbalán en Café y Teoremas, la alumna Marta Herrera de 4º ESO desarrolla la siguiente presentación:

Ene 22 2017

Área de una esfera

En Matemáticas Cercanas encontramos esta gráfica animación sobre el cálculo del área de una esfera:

Ene 17 2017

La caseta de Perico: un nuevo cuento con Geogebra

La web MatemaTICinfantil ha añadido un nuevo recurso. Se trata de La caseta de Perico, un nuevo cuento interactivo desarrollado con Geogebra para trabajar contenido matemáticos en educación infantil. En este caso, a María le han regalado un perrito y quiere construirle una casa, con la ayuda de sus amigos los polígonos. Se utilizan el cuadrado, el triángulo y el rectángulo, en diferentes tamaños y posiciones. En el último nivel, se deben distinguir entre otras figuras, no siempre poligonales, como el pentágono, el hexágono, el círculo o el óvalo.
El cuento tiene cuatro niveles de dificultad que permiten graduar los contenidos que se trabajan, y está pensado para se usado entre los 3 y los 5 años.

Ene 12 2017

Hacer un Tangram en clase

 

Los alumnos de PMAR I del IES Valle del Jiloca, durante la primera evaluación, han realizado un puzzle Tangram en marquetería.

Los objetivos planteados incluían la utilización práctica de los aprendizajes matemáticos obteniendo un producto de carácter lúdico como es el Tamgram. Ha supuesto un proyecto completo en el que el alumnado ha gestionado su tiempo en los siguientes procesos:

  • Elaboración de un documento con las distintas fases a realizar en el proyecto.
  • Búsqueda de información acerca del Tangram, orígenes, modelos, materiales, etc. Estas búsquedas se han realizado haciendo uso del aula de informática.
  • Diseño de bocetos del puzzle, teniendo en cuenta las formas de los polígonos y sus medidas para ajustar el tamaño de la caja.
  • Realización de las piezas y de la caja, teniendo en cuenta las medidas necesarias.
  • Pintado de las piezas y decoración de la caja.

La experiencia ha sido llevada a cabo por la profesora Gemma Rabanaque, que imparte el Ámbito Práctico.

En las fotografías se puede apreciar el resultado: un estupendo juego de Tangram para cada estudiante.

 

 

Como se observa en la foto, el juego amarillo y rojo está preparado para personas con movimiento de las extremidades superiores limitado, ya que cuenta con «tiradores» para facilitar la recogida de las piezas.

Finalemente, el alumnado ilustró un cuento intercalando figuras hechas con sus propios Tangram y perfiladas sobre papel, recortando un collage que se puede apreciar en la siguiente fotografía. Está colocado en la entrada del Instituto:

Por último aquí os dejamos a los alumnos que han realizado todo este trabajo:

Ene 08 2017

Cuéntame un cuento… con Geogebra

El grupo Matematicinfantil lleva más de un lustro elaborando materiales para Infantil utilizando el software Geogebra. Desde sus inicios, cada curso van incorporando actividades con nuevos formatos o elementos. En esta ocasión la novedad son los cuentos interactivos. La incorporación de audio a las construcciones que van elaborando permiten conjugar varias habilidades en una misma actividad. De momento solo hay dos disponibles: Vamos en tren y Lúa se ha escapado. En ambos se utilizan pictogramas de ARASAAC para indicar las acciones iniciales y de desarrollo del cuento, aunque es fundamentalmente el audio quien articula la actividad, que no siempre es igual. Esperamos que estos materiales sean de utilidad en las aulas de Infantil.

 

Dic 26 2016

Tablas de multiplicar II

Geogebra es una excelente herramienta para abordar situaciones como la comentada en la entrada Tablas de multiplicar I.

El uso del comando Secuencia permite en pocos pasos plantear un escenario en el que se pueden ir observando las distintas configuraciones que  van apareciendo al variar los puntos y/o al cambiar de tabla.

La numeración de los puntos solo aparece cuando hay menos de 100, por una cuestión de abigarramiento en la imagen que no permite discernir unos de otros.

El deslizador Número de puntos (N), está acotado entre 10 y 1000 para que puedan verse configuraciones con grandes números de puntos y tablas de números elevados. A su vez, si se quiere visualizar un número de puntos determinado puede hacerse introduciendo el número en la casilla de entrada disponible debajo del deslizador. Dos botones permiten animar el número de puntos para ir visualizando como se configura la tabla de un número.

El siguiente deslizador, t,  corresponde al del número cuya tabla de multiplicación se está visualizando. En este caso el deslizador está acotado entre 2 y N/2. También se dispone de una casilla de entrada para poder escribir la tabla que se quiere visualizar y dos botones que permiten iniciar y detener la animación de este deslizador.

Con un número elevado de puntos las tablas de números grandes ofrecen una imagen espectacular.

N545-t181 Tabla de 181 con 545 puntos en la circunferencia.

N767-t549

Tabla del 549 módulo 767

N926-t584

Tabla del 584 módulo 926

 

En el applet  aparecen dos botones verdes en los que se lee Con decimales y Sin decimales y que hacen que se vayan dibujando las tablas de cualquier número decimal o solamente las de los números enteros. Se ha incluido el de los números decimales porque así se puede visualizar la transición de una tabla a otra.

Por ejemplo, eligiendo  100 puntos, veamos como se visualiza el paso de la tabla del 2 a la del 3:

 

Tabla del 2

Tabla del 2

Tabla del 2.2

Tabla del 2.2

Tabla del 2.4

Tabla del 2.4

Tabla del 2.6

Tabla del 2.6

paso2-8

Tabla del 2.8

Tabla del 3

Tabla del 3

 

Moviendo los deslizadores o animándolos se obtienen diseños espectaculares, y todo a partir de unas simples tablas de multiplicar.

 

“Esta entrada participa en la Edición 7.9 del Carnaval de Matemáticas, que en esta ocasión organiza el blog de José Luis Muñoz.

Dic 23 2016

Tablas de multiplicar I

De vez en cuando las redes sociales te acercan páginas web que ofrecen unos materiales estupendos. Es el caso del canal de video MicMaths de Mickäel  Launay.

Uno de los videos que ofrece en su canal, La face cachée des tables de multiplication,  nos muestra una curiosa e interesante forma de acercarnos y visualizar las tablas de multiplicar.

La idea es simple: Sobre una circunferencia en la que se pueden señalar tantos puntos numerados, como se quiera (cuantos más se pongan más espectacular es el resultado), se trata de ir uniendo cada uno con el resultado de su multiplicación por el número de la tabla que se esté representando. Es decir, si queremos visualizar la tabla del 2 y tenemos señalados 10 puntos en la circunferencia y numerados de 0 a 9, iremos dibujando los segmentos que van del punto 1 al 2 (2 x 1 = 2), otro del 2 al 4 (2 x 2 = 4) y así sucesivamente. Cuando lleguemos a números que pasan del número de puntos, señalaremos el resto de la división del resultado de la multiplicación entre el número de puntos. En nuestro ejemplo, por ejemplo al punto 6 le corresponderá el 2 (2 x 6=12 = 10 +2), al 7 el 4, etc. En definitiva lo que hacemos es construir la tabla del 2 congruente módulo 10. Al aumentar el número de puntos o cambiar de tabla, conseguiremos la tabla congruente módulo el número de puntos.

Así, con 10 puntos, (tabla del 2, módulo 10)

tabla del 2 con 10 puntos

Al aumentar el número de puntos, nos encontramos con la primera sorpresa (tabla del 2 con 300 puntos)

tabla del 2 con 300 puntos

Que continúa al pasar a la tabla del 3 (tabla del 3 con 300 puntos)

tabla del 3 con 300 puntos

Sigue con la del 4 (tabla del 4 con 300 puntos)

tabla del 4 con 300 puntos

Y nos permite predecir cómo será la tabla del 5, del 6, etc…

tabla del 5 con 300 puntos tabla del 6 con 300 puntos

…. O la del 20  (tabla del 20 con 300 puntos).

tabla del 20 con 300 puntos

 

¡Maravilloso!

En inglés…

Esta entrada participa en la Edición 7.9 del Carnaval de Matemáticas, que en esta ocasión organiza el blog de José Luis Muñoz.

Dic 21 2016

Levitation

 

 

Dic 18 2016

Serie microrrelatos – 1: Álgebra amoroso

 

 

algebraamoroso