Nov 12 2016

Cuento interactivo para Ed. Infantil

La web MatemaTICinfantil ha publicado la actividad «Nos vamos en tren«, con la novedad de que utiliza el formato de cuento para su desarrollo.

Implementada con Geogebra como todas las demás, esta actividad incluye un botón que activa el audio, desarrollándose el cuento a lo largo de cuatro fases, en cada una de las cuales el alumnado debe ejecutar una acción. En concreto, trabaja con los ordinales y las clasificaciones, utilizando una pequeña historia en la que tres animales deben subir al tren. Cuando el cuento acaba, éste se marcha.

Está indicada para alumnado entre 3 y 4 años (1º y 2º Ed. Infantil)

Pincha en la imagen para acceder a la página.

MatemaTICinfantil ofrece más de 150 actividades interactivas para trabajar los contenidos lógico-matemáticos en las primeras etapas de la educación, o sea, Ed. Infantil y primeros cursos de Ed. Primaria. Están pensados para desarrollar una clase con la pizarra digital interactiva, en gran grupo, o para trabajar en pequeño grupo o individualmente con tablets.

Su web permite acceder a estos materiales por unidades didácticas, por bloques temáticos y por edades. Dispone de actividades con el contenido textual trilingüe (inglés, francés y castellano) y algunas de ellas usan pictogramas de ARASAAC en las indicaciones al alumnado. También ofrece vídeos de aplicación en el aula.

Nov 09 2016

Convocatorias

La Sociedad Aragonesa de Profesores de Matemáticas ha convocado dos actividades, una dirigida al alumnado y otra al profesorado.

El 25 de octubre se puso en marcha el IV Concurso de Radionovelas matemáticas (como actividad del programa Conexión Matemática),  en colaboración con el Departamento de Educación del Gobierno de Aragón  y la emisora Aragón Radio. Como novedad respecto a otras ediciones se ha habilitado una modalidad General de participación, en la que cualquier persona que viva en Aragón, no necesariamente vinculada al ámbito educativo, puede participar con un guión radiofónico. El premio consiste en la grabación de la radionovela por locutores profesionales. En la modalidad Escolar, no hay cambios respecto a otras convocatorias: hay que presentar la radionovela grabada de una duración entre 3 y 5 minutos. Es una buena ocasión para movilizar el trabajo interdisciplinar entre varias asignaturas. El plazo de presentación de los trabajos finaliza el 31 de marzo.

Consulta las bases del concurso en este enlace.

La imagen está enlazada con la página de Aragón Radio en la que están todas las radionovelas presentadas en anteriores ediciones.

 

Por otra parte, dirigido al profesorado y estudiantes se ha convocado la II Jornada de Educación Matemática en Aragón, reconocida por el Departamento de Educación con 10 horas de formación. La inscripción es gratuita y se puede hacer desde la página de la Jornada. Se celebrará el viernes 3 de febrero, por la tarde y el sábado 4 de febrero por la mañana en la Facultad de Educación de la Universidad de Zaragoza. Toda la información se encuentra en este enlace.

El espacio dedicado a las comunicaciones de trabajos, experiencias de aula, materiales, etc., está abierto a la participación de todo el que quiera presentar alguna. La presentación de comunicaciones se certificará como ponencia. Y también se quiere «ambientar» el lugar en el que se desarrollará la Jornada, con trabajos realizados con alumnos, Toda la información, en la web.

 

 

 

Nov 06 2016

Moviendo la recta de Euler

r3s1vr4vs3 r3s4vr4vs3 r1s4vr3vs1

En el número 81 de la revista Suma, iniciando la sección CreoGebra José Luis Muñoz mostraba un ejercicio dinámico de sencillo planteamiento: Sobre un punto de una circunferencia dibujamos otra con centro en él, y sobre esta última señalamos otro punto. Se activa el rastro de este último y se animan los dos puntos que están dibujados sobre las circunferencias. Todo ello realizado con Geogebra de manera sencilla permite observar patrones y regularidades en los llamativos dibujos que se generan.

Con esa misma idea, se plantea esta entrada. En el planteamiento anterior hay tres puntos: el centro de la primera circunferencia, el centro de la segunda circunferencia y el tercer punto es el que se coloca sobre esta última. Con tres puntos podemos dibujar el triángulo que forman. Y en él podemos señalar los puntos notables, de los cuales tres nos permiten dibujar la recta de Euler. Activando el rastro de la recta y animando los puntos sobre las circunferencias con distintas velocidades, se obtienen imágenes como las que ilustran esta entrada.

r3s1vr1vs10 r1s4vr5vs1 r3s1vr1vs

En el siguiente applet puedes ir modificando los parámetros y activar puntos notables y recta a voluntad para ir obteniendo distintos dibujos.

 

r3s1vr1vs2b

Estaa imagen corresponde a una de las anteriores, pero solo muestra el trazo de baricentro, circuncentro y ortocentro, ¿la reconoces?

 

 

Esta entrada participa en la Edición 7.7 del Carnaval de Matemáticas, que en esta ocasión organiza Los Matemáticos no son gente seria.

Nov 04 2016

Marcando el terreno con una terna pitagórica

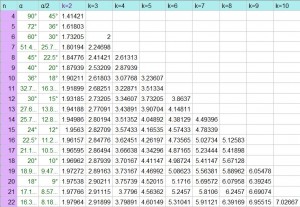
Experiencia didáctica en el IES Valle del Jiloca (Calamocha) en la que un grupo de alunmnos debía marcar sobre la pista deportiva del instituto un cuadrado de 5 metros de lado.

Nivel: 2º – 3º ESO En este caso se llevó a cabo en el Taler de Matemátias de 3º ESO.

Objetivo: Conocer el concepto de «terna pitagórca», su relacion con el Teorema de Pitágoras, y cómo usarlas apara dibujar ángulos rectos. Aprender el significado del error absoluto y relativo, así como la diferencia entre ambos.

Contenidos: Teorema de Pitágoras. Un poco de historia de las matemáticas. Cálculo de errores.

Metodología:

1º Visualización del vídeo en el que se explica cómo los antiguos egipcios utilizaban la terna pitagórica 3 – 4 – 5 para dibujar los campos después de las crecidas del Nilo.  Universo Matemático 1: Pitágoras, mucho más que un Teorema (especialmente entre los minutoes 6 y 8)

2º Elaboración de una cuerda de 12m con marcas cada metro para poder «montar» un triángiulo rectángulo con la mecionada terna.

3º Salida al patio para dibujar el cuadrado, yendo de un ángulo al siguiente contiguo hasta completar los 4. Se evitó expresamente el paralelismo con las marcas del campo deportivo para evitar facilidades. En primer lugar se marcaba el ángulo mediante dos segmentos dibujados con tiza y posteriormente se alargaban la medida necesaria. El único instrumento de medida era la cuerda marcada con la terna (sin cintas métricas ni dispositivos de medir ángulos)

4º Medida del error cometido. Al llegar al último ángulo se comprobó que el «cuadrado» trazado no se podía cerrar, debido a la desviación del dibujo. Se midió la distancia que faltaba por cerrar y se comparó con el perímetro que debería haber tenido. Ya en clase se hizo el cálculo de este error relativo.

Materiales necesarios:

Proyector y ordenador para visualizar el vídeo, cuerda (12 m), cinta de color para marcar la terna, tiza para dibujar en el suelo, calculadora para evalar el error cometido.

Resultados obtenidos:

El cuadrado no se cerró por 8,5 cm en un perímetro de 4·5=20 m. El error relativo cometido sería de:

 

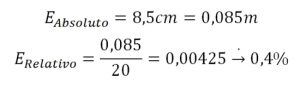
error-terna-pit

Valoración de la actividad:

La valoración es muy positiva por los siguientes motivos:

El alumnado desarrolla las matemáticas de forma aplicada a un caso real. Las «ve» fuera del aula, y trabaja con ellas sin apenas usar el lápiz y el papel.

Se comprende la dificultad de llevar la teoría a la práctica, constatando que cometer un error es algo inherente al hecho de medir. Además, la actividad facilita la comprensión de la diferencia entre error absoluto y error relativo, así como la necesidad de éste último para comprender el alcance del problema.

Si no lleuve, se toma el sol, que siempre aporta vitamina B6

20160518_084010

Comprobando la terna construida con corden en la esquina el campo deportivo.

 20160518_094954 20160518_095547 20160518_094723   20160518_094512

Esta entrada participa en la Edición 7.7 del Carnaval de Matemáticas, que en esta ocasión organiza Los Matemáticos no son gente seria.

Nov 01 2016

Matemáticas en Tutoría

Proponemos hoy una actividad para desarrollar en una sesión de Tutoría entre 1º y 4º de ESO. Se trata de hacer una reflexión ´sobre el uso personal del tiempo, con el objetivo de mejorar la actividad de estudio.
La propuesta contempla el trabajo con una ficha en papel, para calcular el porcentaje de tiempo que se dedica diariamente las diferentes actividades, así como la realización de un diagrama de barras y/o sectores (según el nivel) que refleje dicho estudio. Posteriormente, se propone la recogida de todos los datos en una hoja de cálculo como ésta para extraer la dedicación media de la clase a las diferentes tareas. Se propone así mismo imprimir las gráficas de los resultados globales para hacer un seguimiento de la evolución, repitiendo el estudio trimestralmente (en este caso, apoyándose en la hoja de cálculo para que sea más breve).

aquededicomitiempo

aquededicomitiempo

Oct 29 2016

Trampantojo

En la calle del Sombrerete, del madrileño barrio de Lavapiés, encontramos este maravilloso trampantojo en La Casa de la Vela. Combina la medida del tiempo a través de la sombra solar, con la cotidianeidad de tener la ropa a su calor.

relojsollavapies

La inscripción dedica el reloj, que data de 1985, a los vecinos del barrio de Embajadores.

Oct 26 2016

Corona circular sobre polígonos

Continuando con las entradas dedicadas a las coronas circulares en Matryc (Corona circular  y  Círculos con en-Cantor)  en este mismo blog, nos plantemos una pequeña cuestión surgida al estudiar en clase el incentro y el baricentro de un triángulo, particularizando al caso de polígonos regulares y generalizando a cualquier clase de polígono.

En un polígono regular podemos trazar una circunferencia que pase por todos los vértices del mismo (circunferencia circunscrita) y otra que sea tangente a todos los lados del polígono (circunferencia inscrita). Entre ellas forman una corona circular en la  que el polígono queda encajado.  La pregunta es cuánto vale el área de esa corona circular y en qué forma depende del número de lados que tenga el polígono.

corona-triangulo corona-cuadrado  corona-penta corona-hexa

 

Llamaremos r al radio de la circunferencia circunscrita, que va desde el centro del polígono hasta un vértice y ap al radio de la circunferencia inscrita ya que coincide con la apotema del polígono. Se forma el triángulo rectángulo de la figura.

Aplicando el teorema de Pitágoras, el área de la corona circular será:

\displaystyle A=\pi r^{2}-\pi ap^{2}=\frac{\pi}{4}l^{2}

 

Es decir, el área de la corona no depende del número de lados del polígono sino que solamente depende del valor del lado. Equivale al área de un círculo cuyo diámetro coincida con el lado.

Oct 23 2016

Dibujar fractales

La aplicación DOODAL permite dibujar fractales de una manera muy sencilla. La pantalla de trabajo es simple y las herramientas sencillas de manejar. Lo puedes ver en este video:

Oct 20 2016

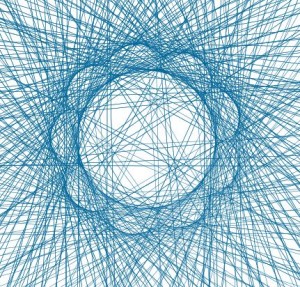
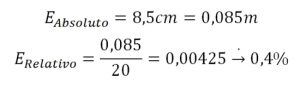
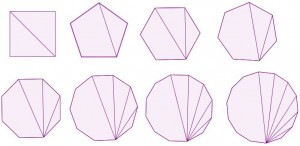
Diagonales

De las \displaystyle\frac{n(n-3))}{2} diagonales que tiene un polígono de n lados, no todas tienen la misma longitud, pues depende de los vértices que deja entre sus extremos. Es decir, la diagonal que une un vértice con el que se encuentra dos posiciones más a la derecha, es distinta que la que une ese vértice con otro situado tres o cuatro posiciones en el mismo sentido (suponiendo un número de lados lo suficientemente elevado).

diagonales

En esta entrada vamos a ver cual es la relación de cada una de las diagonales (d)  con el lado (l) en un polígono regular de n lados.

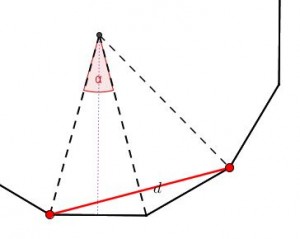
diagonal1

Comencemos por la diagonal más pequeña del polígono, la que une un vértice con el situado dos vértices hacia un lado. La hemos llamado d.

El ángulo central es \displaystyle \alpha =\frac{2\pi}{n}

Fijándonos en los triángulos señalados, se deduce que

\displaystyle sen\alpha =\frac{d/2}{r}    y    \displaystyle sen\frac{\alpha}{2} =\frac{l/2}{r}

De donde se deduce que \displaystyle \frac{d}{l}=\frac{sen\alpha }{sen\frac{\alpha }{2}}

 

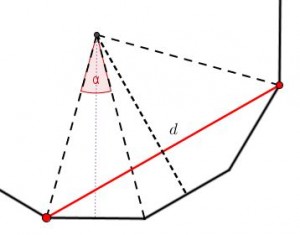diagonal2 Si consideramos una diagonal mayor, por ejemplo la que une un vértice y un tercero a su derecha, como en la imagen y aplicamos el mismo esquema que hemos seguido en el caso anterior, observamos que:

\displaystyle sen\frac{3\alpha}{2} =\frac{d/2}{r}    y    \displaystyle sen\frac{\alpha}{2} =\frac{l/2}{r}

De donde se deduce que \displaystyle \frac{d}{l}=\frac{sen\frac{3\alpha }{2}}{sen\frac{\alpha }{2}}

 

 

Si calculamos esta proporción con la siguiente diagonal, la que abarca 4 lados, obtendremos \displaystyle \frac{d}{l}=\frac{sen\frac{4\alpha }{2}}{sen\frac{\alpha }{2}}

Y por tanto podremos generalizar que para un polígono de n lados, la razón de cada diagonal con el lado es:

\displaystyle \frac{d}{l}=\frac{sen\frac{k\pi }{n}}{sen\frac{\pi }{n}} para valores de k entre 2 y la parte entera de n/2.

Para terminar, en la tabla se muestran las relaciones de todos los polígonos desde el cuadrado hasta el icosakaidígono. (k es el número de lados que abarca la diagonal correspondiente).

diagonalestabla

Oct 17 2016

Tipografía geométrica

Danilo Gusmão Silveira ofrece de manera gratuita esta tipografía decorativa,  inspirada en las líneas y formas del universo de la geometría: líneas rectas, curvas, ángulos, planos, círculos, circunferencias, triángulos, cuadrados, etc.

 

Se puede descargar en este enlace

Nota: La fuente viene en formato .ai, para pasarla a un formato ttf se puede utilizar un conversor online como este