De vez en cuando las redes sociales te acercan páginas web que ofrecen unos materiales estupendos. Es el caso del canal de video MicMaths de Mickäel Launay.
Uno de los videos que ofrece en su canal, La face cachée des tables de multiplication, nos muestra una curiosa e interesante forma de acercarnos y visualizar las tablas de multiplicar.
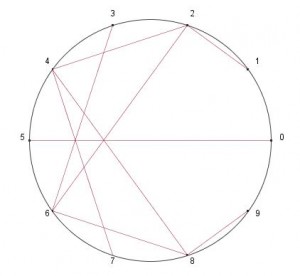
La idea es simple: Sobre una circunferencia en la que se pueden señalar tantos puntos numerados, como se quiera (cuantos más se pongan más espectacular es el resultado), se trata de ir uniendo cada uno con el resultado de su multiplicación por el número de la tabla que se esté representando. Es decir, si queremos visualizar la tabla del 2 y tenemos señalados 10 puntos en la circunferencia y numerados de 0 a 9, iremos dibujando los segmentos que van del punto 1 al 2 (2 x 1 = 2), otro del 2 al 4 (2 x 2 = 4) y así sucesivamente. Cuando lleguemos a números que pasan del número de puntos, señalaremos el resto de la división del resultado de la multiplicación entre el número de puntos. En nuestro ejemplo, por ejemplo al punto 6 le corresponderá el 2 (2 x 6=12 = 10 +2), al 7 el 4, etc. En definitiva lo que hacemos es construir la tabla del 2 congruente módulo 10. Al aumentar el número de puntos o cambiar de tabla, conseguiremos la tabla congruente módulo el número de puntos.
Así, con 10 puntos, (tabla del 2, módulo 10)
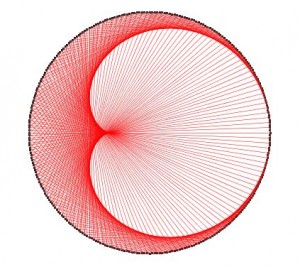
Al aumentar el número de puntos, nos encontramos con la primera sorpresa (tabla del 2 con 300 puntos)
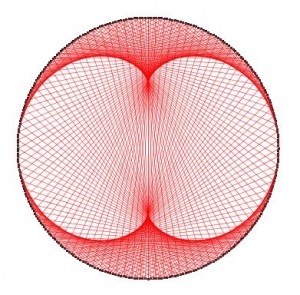
Que continúa al pasar a la tabla del 3 (tabla del 3 con 300 puntos)
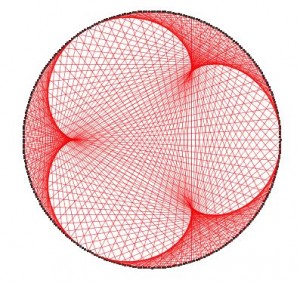
Sigue con la del 4 (tabla del 4 con 300 puntos)
Y nos permite predecir cómo será la tabla del 5, del 6, etc…
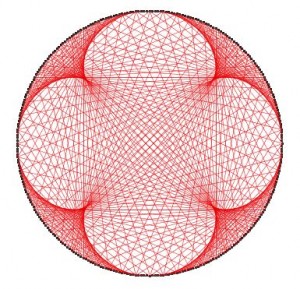
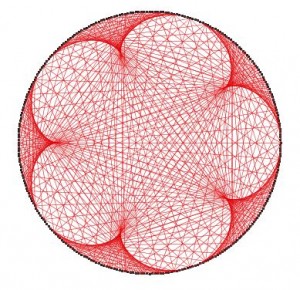
…. O la del 20 (tabla del 20 con 300 puntos).
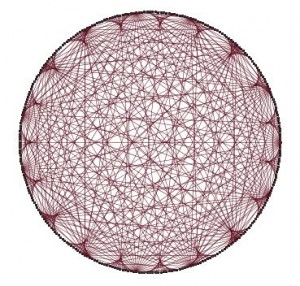
¡Maravilloso!
En inglés…
