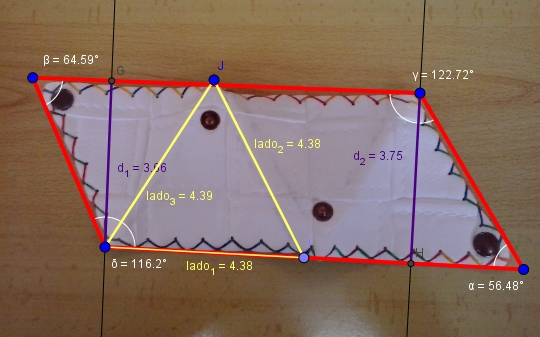
Hoy proponemos una actividad para el aula: la construcción de un monedero con forma de romboide.
Objetivo: Aplicar los conocimientos de geometría a un objeto cotidiano.
Contenidos: Cuadriláteros (romboide), teorema de Pitágoras aplicado al cálculo de áreas.
Nivel: 3º ESO
Descripción: Se trataría de construir un monedero como el de las imágenes, recortando fieltro y cerrando con una tira de velcro. El que podemos ver ha sido realizado en un taller e Disminuidos Físicos de Aragón.



Si observamos la imagen en la que está desplegado, podemos ver que se trata de un romboide en el que un lado es el doble de largo que el otro, ya que está formado por cuatro triángulos equiláteros, condición imprescindible para que el monedero cierre bien y no se caigan las monedas. Bastan dos dobleces para formalo, dejando el último triángulo como tapa.
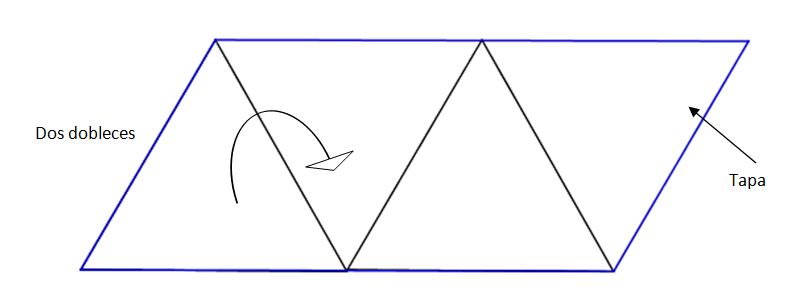
Esta configuración geométrica permitiría a los alumnos calcular el área del romboide en función de la longitud del lado más pequeño, incluso sin conocer la expresión de la misma.
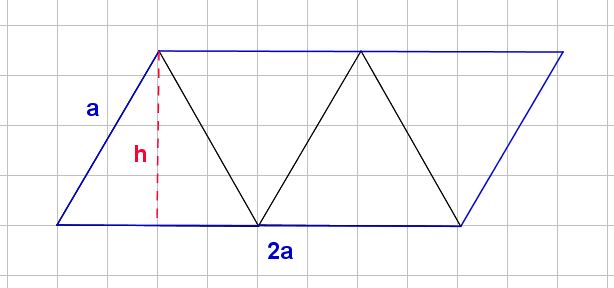
Con el teorema de Pitágoras, pueden obtener la expresión de la altura del triángulo:
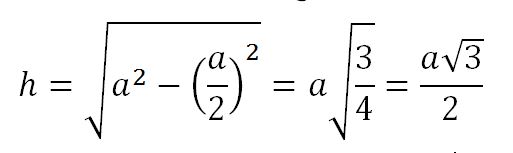
Con lo que podrían calcular el área de uno de los triángulos:
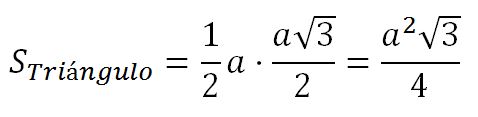
Y por tanto, la de todo el romboide:
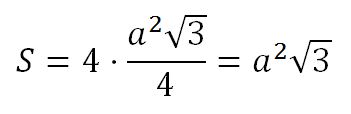
Claro que, una cosa son los modelos y otra la realidad. ¿Era realmente un romboide el monedero de nuestras imágenes?: