En busca de un número

En esta ocasión, el problema planteado es para 3º ESO y como otras veces, aparecen formas de resolverlo diferentes. El problema es:

Encuentra dos números naturales tales que los dos séptimos de uno coincidan con los tres octavos del otro.

De nuevo el álgebra al rescate: si x es uno de los números e y el otro, 

Y de ahí se obtiene de forma rápida que x=21 e y=16 son solución de problema.

En este caso una función lineal representa las posibles soluciones de las que solo serán válidas aquellas que pasen exactamente por los puntos de intersección de la cuadrícula.

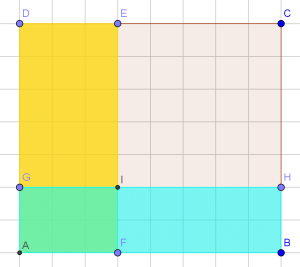
Pero hay otras alternativas. Virginia busca el denominador común de las dos fracciones: 56.  Y ahora calcula los 2/7 de 56 que son 16 y los 3/8 de 56 que son 21 y ya lo tiene, sin necesidad de x ni y.  El dibujo lo muestra gráficamente. Los rectángulos amarillo y azul son las soluciones.

Irene sin embargo utiliza otro razonamiento. “Para averiguarlo tenemos que encontrar un número que al multiplicarlo por 2 nos de lo mismo que al multiplicar otro número por 3”. Ella elige el 30  (15 x 2 = 10 x 3). Y continúa “los números 15 y 10 tenemos que multiplicarlos por sus números respectivos (el 7 para el 15 y el 8 para el 10) y se obtiene  15 x 7 =105   y  10 x 8 = 80”.

No son los números más pequeños que cumplen la propiedad, pero los hubiera conseguido si en lugar de elegir 15 y 10 elige 3 y 2.