Hace poco tiempo me encontré con el siguiente ejercicio:
Dibujar un círculo de la misma área que una corona circular dada
El cálculo del radio de ese círculo es rápido: si el radio exterior es R y el interior r, se deduce que el radio del círculo que buscamos, x, es
Pero al decir dibujar, uno piensa en regla y compás, al estilo clásico, y en estos tiempos, estas herramientas se llaman Geogebra. Así que buscando distintas maneras de llegar a la solución ofrecemos tres soluciones al problema relaizadas con este software. (Enlace)
La primera de ellas, se basa en la aplicación directa del teorema de Pitágoras.
El radio buscado es el cateto del triángulo rectángulo cuya hipotenusa es R y el otro cateto es r. Partiendo de un segmento de longitud r (BC) , trazamos una perpendicular a dicho segmento por uno de los extremos y desde el otro extremo se dibuja una circunferencia de radio R. La intersección de estos dos objetos nos dará el tercer vértice del triángulo rectángulo que buscamos, D. El círculo buscado tiene por radio CD.
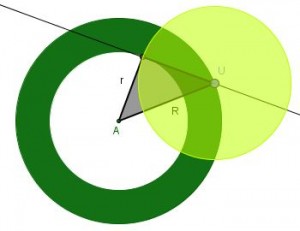
Sobre la corona, podemos seguir los siguientes pasos. Desde un punto cualquiera de la circunferencia exterior se traza una tangente a la circunferencia interior. El punto de tangencia, el centro de la corona y el primer punto elegido, forman un triángulo rectángulo, uno de cuyos catetos es r y la hipotenusa R.
El siguiente método se basa en el teorema de la altura. Para ello se dibuja una semicircunferencia de radio R. Desde un extremo del diámetro se señala el segmento de longitud R+r (EF) , el resto del diámetro (FG) mide entonces, R-r. La perpendicular al diámetro por F, interseca a la semicircnferencia en el punto I. El radio buscado es el segmento FI.
El triángulo EIG es rectángulo en I. El cuadrado de la altura x2 es igual al producto de llas proyecciones de los catetos sobre la hipotenusa (R+r)(R-r).
Y de ahí se deduce fácilmente que x es el radio del círculo buscado.
La tercera solución se basa en la cuadratura de un rectángulo de lados R+r y R-r. Una solución consistiría en aplicar el método anterior, pero vamos a seguir una regla que aparece en los textos Salvasutras de las matemáticas brahmánicas.
“Para construir un cuadrado equivalente (en área) a un rectángulo ABCD dado, llévense los lados menores sobre los mayores de manera que AF = AB =BE =CD y trácese HG mediatriz de los segmentos CE y DF; prolónguese EF hasta K, GH hasta L y AB hasta M, de manera que FK = HL = FH = AM y trácese la recta LKM. Constrúyase ahora un rectángulo con diagonal igual a LG y con su lado más corto igual a HF, entonces el lado más largo de este rectángulo es el lado x del cuadrado buscado”
La demostración de esta construcción será:
Y aplicando este método a nuestra situación, obtenemos:
