Esta imagen está construida con tres métodos distintos, que dan solución al problema de inscribir un cuadrado de lado dado en otro cuadrado fijo. Se completa la imagen con una simple simetría que construye el cuarto cuadrado amarillo.
Sea pues un cuadrado fijo de lado 
Método 1: La aplicación directa del teorema de Pitágoras.
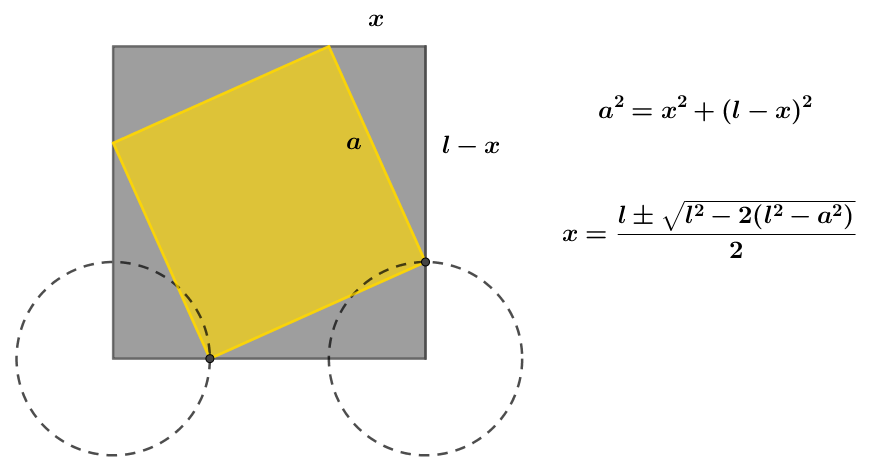
Método 2: Problema 292 del libro Problemas gráficos y numéricos de geometría (1312 problemas resueltos), de M. García Ardura, Madrid, 1957.
El procedimiento comienza con trazar la bisectriz de un ángulo recto exterior del cuadrado, y dibujar una circunferencia de radio la distancia dada con centro en el vértice contiguo. La intersección de los dos elementos construidos nos proporciona un punto que junto al vértice que ha servido de centro de la circunferencia determinan una recta. El punto se proyecta perpendicularmente sobre el lado y trazando una recta paralela a la anterior por ese punto, se consigue el lado del cuadrado inscrito.
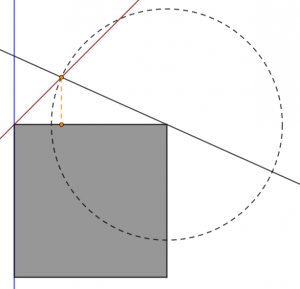
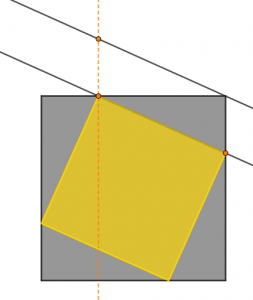
Método 3: Dibujar un cuadrado del lado que se quiere concéntrico con el dado y luego girarlo el ángulo necesario. Para encontrar el ángulo basta trazar un arco de circunferencia con centro en el cuadrado y radio hasta el vértice del construido. Eso determina sobre el lado del cuadrado fijo un punto, que permite encontrar el ángulo de giro.
Si se te ocurre otra manera de resolverlo, cambiamos la simetría para rellenar el cuarto cuadrado.
