Sobre un triángulo cualquiera, señalamos un punto en el interior. Unimos ese punto con cada uno de los vértices y tendremos tres triángulos. Calculamos y dibujamos el baricentro de cada uno de esos triángulos y los unimos. Obtenemos otro triángulo.
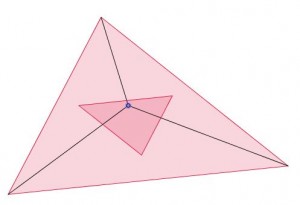
Al desplazar el punto por el interior se observa que el nuevo triángulo no cambia de dimensiones, solo de posición. Por tanto, la relación de las áreas se mantiene independientemente de donde esté situado el punto interior.
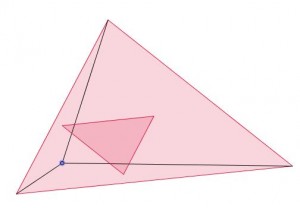
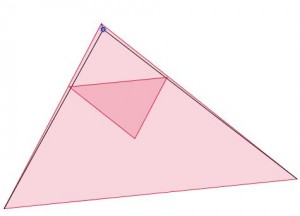
Ocurre lo mismo si realizamos el proceso sobre un cuadrílátero o un pentágono o cualquier otro polígono.
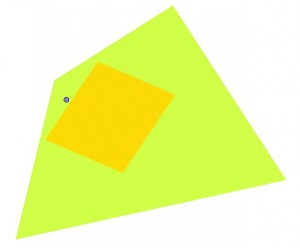
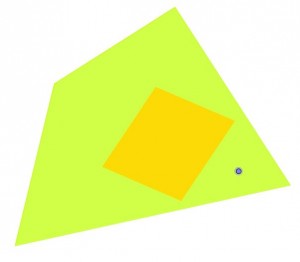
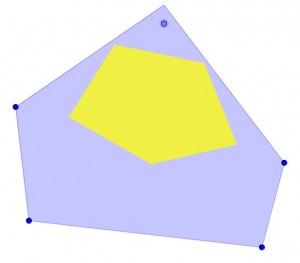
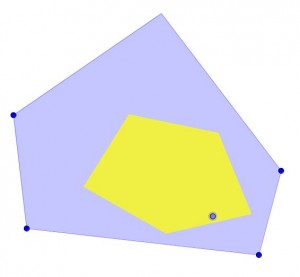
Nos centramos en los polígonos regulares, y con Geogebra elaboramos un applet que muestre qué ocurre en ellos.
En el applet se puede ver que al mover el punto amarillo, el polígono baricéntrico resultante no cambia. Además se muestra la relación entre el área del polígono que se forma con los baricentros y lal del polígono de partida. Veamos cuál es esa relación.
Para ello partimos del caso del triángulo de vértices A, B y C como muestra la imagen:
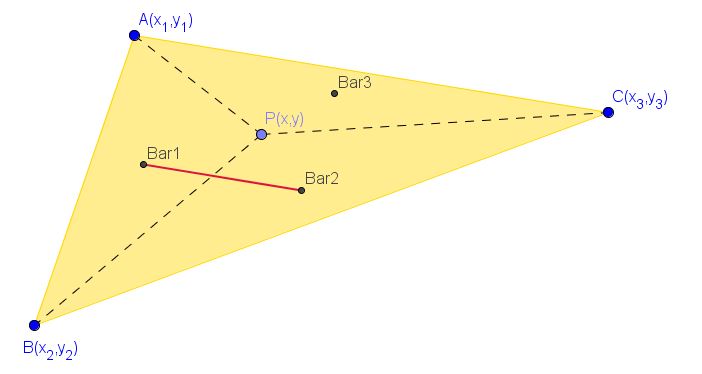
Calculamos las coordenadas de los baricentros (nos basta con Bar1 y Bar2) para hallar el valor del segmento que une esos dos puntos.
Con los otros lados ocurrirá lo mismo, en conclusión, para el triángulo, el lado del triángulo baricéntrico es la tercera parte del lado del triángulo de partida.
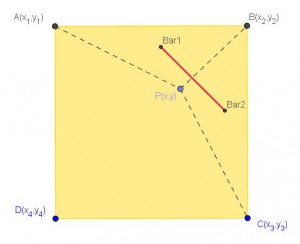Veamos qué ocurre en el caso del cuadrado. Siguiendo el mismo método que en el caso del triángulo, llegamos a la misma expresión, pero en este caso, el segmeto AC no es el lado del cuadrado sino la diagonal del cuadrado,
Si pasamos al pentágono el segmento AC será de nuevo una diagonal del pentágono. Con el hexágono ocurrirá lo mismo, aunque en este polígono las diagonales tienen medidas distintas. La que nos aparece en la expresión es la diagonal más corta del hexágono. Y lo mimo ocurrirá con polígonos de un número mayor de lados.
En consecuencia, el lado del polígono baricéntrico, es la tercera parte de la diagonal más corta del polígono de partida. Calculémosla.
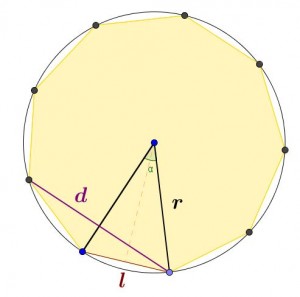Supongamos un polígono regular de n lados inscrito en una circunferencia.
El segmento d y el radio se cortan perpendicularmente, el radio es mediatriz de ese segmento.
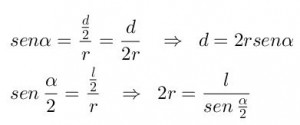
De donde, sustituyendo, se encuentra el valor de la diagonal de menor longitud con respecto al lado del polígono.
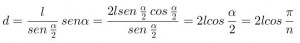
Por tanto el lado del polígono baricéntrico, la rercera parte del valor de la diagonal,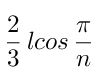 
Así pues la relación entre los lados del polígono original y el polígono baricéntrico es:
Y por tanto la relación entre las áreas será su cuadrado,
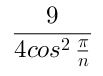
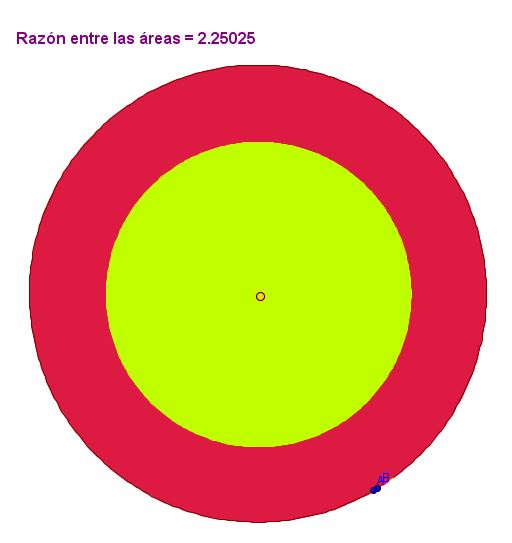
Este resultado se puede ir comprobando directamente sobre el applet, ya que este calcula el cociente entre las dos áreas. Si hacemos crecer el número de lados la relación entre las áreas tiende a 9/4.
En el caso límite el polígono se convertiría en un círculo y el polígono baricéntrico sería otro, con lo que tendríamos una corona circular, de forma que la relación entre los radios de las circunferencias sería 3/2. Esto recuerda la relación en que el baricentro divide la mediana en tres partes, una doble que la otra.
