Continuando con las entradas dedicadas a las coronas circulares en Matryc (Corona circular y Círculos con en-Cantor) en este mismo blog, nos plantemos una pequeña cuestión surgida al estudiar en clase el incentro y el baricentro de un triángulo, particularizando al caso de polígonos regulares y generalizando a cualquier clase de polígono.
En un polígono regular podemos trazar una circunferencia que pase por todos los vértices del mismo (circunferencia circunscrita) y otra que sea tangente a todos los lados del polígono (circunferencia inscrita). Entre ellas forman una corona circular en la que el polígono queda encajado. La pregunta es cuánto vale el área de esa corona circular y en qué forma depende del número de lados que tenga el polígono.
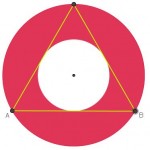



Llamaremos r al radio de la circunferencia circunscrita, que va desde el centro del polígono hasta un vértice y ap al radio de la circunferencia inscrita ya que coincide con la apotema del polígono. Se forma el triángulo rectángulo de la figura.

Aplicando el teorema de Pitágoras, el área de la corona circular será:
Es decir, el área de la corona no depende del número de lados del polígono sino que solamente depende del valor del lado. Equivale al área de un círculo cuyo diámetro coincida con el lado.
