Diagonales

De las  diagonales que tiene un polígono de n lados, no todas tienen la misma longitud, pues depende de los vértices que deja entre sus extremos. Es decir, la diagonal que une un vértice con el que se encuentra dos posiciones más a la derecha, es distinta que la que une ese vértice con otro situado tres o cuatro posiciones en el mismo sentido (suponiendo un número de lados lo suficientemente elevado).

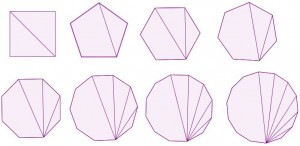
En esta entrada vamos a ver cual es la relación de cada una de las diagonales (d)  con el lado (l) en un polígono regular de n lados.

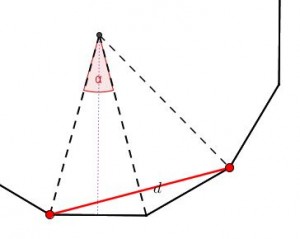
Comencemos por la diagonal más pequeña del polígono, la que une un vértice con el situado dos vértices hacia un lado. La hemos llamado d.

El ángulo central es 

Fijándonos en los triángulos señalados, se deduce que

   y    

De donde se deduce que 

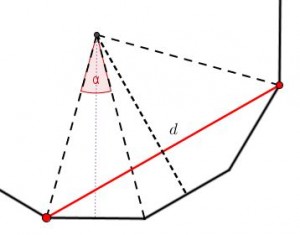 Si consideramos una diagonal mayor, por ejemplo la que une un vértice y un tercero a su derecha, como en la imagen y aplicamos el mismo esquema que hemos seguido en el caso anterior, observamos que:

   y    

De donde se deduce que 

Si calculamos esta proporción con la siguiente diagonal, la que abarca 4 lados, obtendremos 

Y por tanto podremos generalizar que para un polígono de n lados, la razón de cada diagonal con el lado es:

para valores de k entre 2 y la parte entera de n/2.

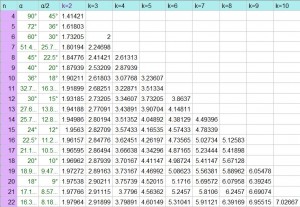
Para terminar, en la tabla se muestran las relaciones de todos los polígonos desde el cuadrado hasta el icosakaidígono. (k es el número de lados que abarca la diagonal correspondiente).