


En el número 81 de la revista Suma, iniciando la sección CreoGebra José Luis Muñoz mostraba un ejercicio dinámico de sencillo planteamiento: Sobre un punto de una circunferencia dibujamos otra con centro en él, y sobre esta última señalamos otro punto. Se activa el rastro de este último y se animan los dos puntos que están dibujados sobre las circunferencias. Todo ello realizado con Geogebra de manera sencilla permite observar patrones y regularidades en los llamativos dibujos que se generan.
Con esa misma idea, se plantea esta entrada. En el planteamiento anterior hay tres puntos: el centro de la primera circunferencia, el centro de la segunda circunferencia y el tercer punto es el que se coloca sobre esta última. Con tres puntos podemos dibujar el triángulo que forman. Y en él podemos señalar los puntos notables, de los cuales tres nos permiten dibujar la recta de Euler. Activando el rastro de la recta y animando los puntos sobre las circunferencias con distintas velocidades, se obtienen imágenes como las que ilustran esta entrada.
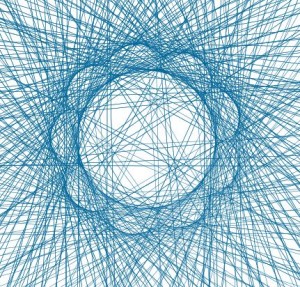


En el siguiente applet puedes ir modificando los parámetros y activar puntos notables y recta a voluntad para ir obteniendo distintos dibujos.
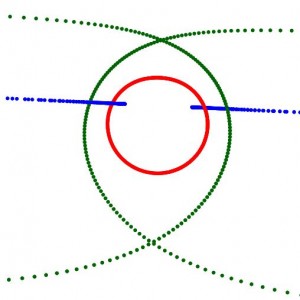
Estaa imagen corresponde a una de las anteriores, pero solo muestra el trazo de baricentro, circuncentro y ortocentro, ¿la reconoces?
Esta entrada participa en la Edición 7.7 del Carnaval de Matemáticas, que en esta ocasión organiza Los Matemáticos no son gente seria.
